Page 159 - Buku Teks Digital Mate KSSM T5

Bab 6 Ketaksamaan Linear dalam Dua Pemboleh Ubah

Bagaimanakah anda menentusahkan konjektur titik dalam suatu rantau yang
memenuhi suatu ketaksamaan linear?
y
Standard
Pembelajaran
2
Membuat dan
x ≥ 1 menentusahkan konjektur
1 tentang titik dalam rantau
x dan penyelesaian bagi
0 1 2 3 O 1 2 3 4 x suatu ketaksamaan linear.
Rajah 1
–1

Rajah 2
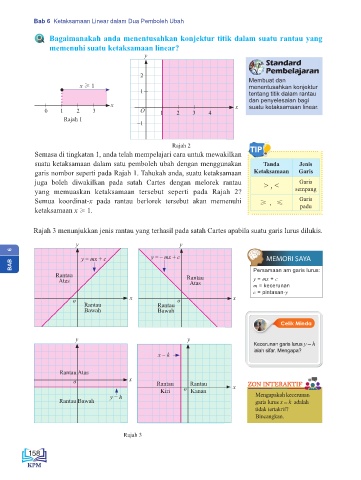
Semasa di tingkatan 1, anda telah mempelajari cara untuk mewakilkan TIP
suatu ketaksamaan dalam satu pemboleh ubah dengan menggunakan Tanda Jenis
garis nombor seperti pada Rajah 1. Tahukah anda, suatu ketaksamaan Ketaksamaan Garis
juga boleh diwakilkan pada satah Cartes dengan melorek rantau > , < Garis
yang memuaskan ketaksamaan tersebut seperti pada Rajah 2? sempang
Semua koordinat-x pada rantau berlorek tersebut akan memenuhi ≥ , ≤ Garis
padu
ketaksamaan x ≥ 1.

Rajah 3 menunjukkan jenis rantau yang terhasil pada satah Cartes apabila suatu garis lurus dilukis.

y y
6 y = – mx + c
BAB y = mx + c MEMORI SAYA

Rantau Rantau Persamaan am garis lurus:
Atas Atas y = mx + c
m = kecerunan
c = pintasan-y
x x
o o
Rantau Rantau
Bawah Bawah
Celik Minda

y y
Kecerunan garis lurus y = h
ialah sifar. Mengapa?
x = k

Rantau Atas
o x Rantau Rantau ZON INTERAKTIF
Kiri o Kanan x
y = h Mengapakah kecerunan
Rantau Bawah garis lurus x = k adalah
tidak tertakrif?
Bincangkan.

Saiz sebenar Rajah 3

158