Page 14 - Microsoft Word - แคลคูลัส.docx

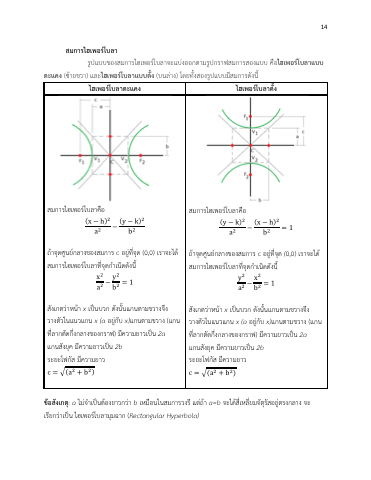
สมการไฮเพอรNโบลา
ตะแคง
ไฮเพอรNโบลาแบบ
14
รูปแบบของสมการไฮเพอรXโบลาจะแบTงออกตามรูปกราฟสมการสองแบบ คือ
(ซ<ายขวา) และ
ไฮเพอรNโบลาแบบตั้ง
(บนลTาง) โดยทั้งสองรูปแบบมีสมการดังนี้
ไฮเพอรNโบลาตะแคง
ไฮเพอรNโบลาตั้ง
สมการไฮเพอรXโบลาคือ
(x−h)" (y−k)" a" − b"
ถ<าจุดศูนยXกลางของสมการ c อยูTที่จุด (0,0) เราจะได< สมการไฮเพอรXโบลาที่จุดกําเนิดดังนี้
x" y"
a" − b" = 1
สังเกตวTาหน<า x เปOนบวก ดังนั้นแกนตามขวางจึง วางตัวในแนวแกน x (a อยูTกับ x)แกนตามขวาง (แกน ที่ลากตัดกึ่งกลางของกราฟ) มีความยาวเปOน 2a แกนสังยุค มีความยาวเปOน 2b
ระยะโฟกัส มีความยาว
c = ;(a" + b")
สมการไฮเพอรXโบลาคือ
(y−k)" (x−h)"
a" − b" =1
ถ<าจุดศูนยXกลางของสมการ c อยูTที่จุด (0,0) เราจะได< สมการไฮเพอรXโบลาที่จุดกําเนิดดังนี้
y" x"
a" − b" = 1
สังเกตวTาหน<า x เปOนบวก ดังนั้นแกนตามขวางจึง วางตัวในแนวแกน x (a อยูTกับ x)แกนตามขวาง (แกน ที่ลากตัดกึ่งกลางของกราฟ) มีความยาวเปOน 2a แกนสังยุค มีความยาวเปOน 2b
ระยะโฟกัส มีความยาว
c = ;(a" + b")
ขKอสังเกตุ: a ไมTจําเปOนต<องยาวกวTา b เหมือนในสมการวงรี แตTถ<า a=b จะได<สี่เหลี่ยมจัตุรัสอยูTตรงกลาง จะ เรียกวTาเปOน ไฮเพอรXโบลามุมฉาก (Rectangular Hyperbola)