Page 17 - Microsoft Word - แคลคูลัส.docx

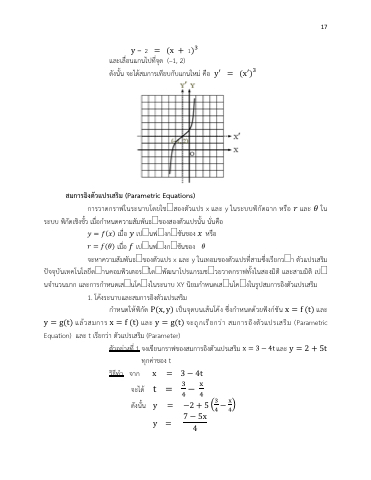
y–2 = (x+1)r และเลื่อนแกนไปที่จุด (–1, 2)
ดังนั้น จะได<สมการเทียบกับแกนใหมT คือ y′ = (x′)r
สมการอิงตัวแปรเสริม (Parametric Equations)
การวาดกราฟในระนาบโดยใชสองตัวแปร x และ y ในระบบพิกัดฉาก หรือ 𝑟 และ 𝜃 ใน ระบบ พิกัดเชิงขั้ว เมื่อกําหนดความสัมพันธของสองตัวแปรนั้น นั่นคือ
𝑦 = 𝑓(𝑥) เมื่อ 𝑦 เปนฟงกชันของ 𝑥 หรือ
𝑟=𝑓(𝜃)เมื่อ𝑓เปนฟงกชันของ 𝜃
จะหาความสัมพันธของตัวแปร x และ y ในเทอมของตัวแปรที่สามซึ่งเรียกวา ตัวแปรเสริม
ปwจจุบันเทคโนโลยีดานคอมพิวเตอรไดพัฒนาโปรแกรมชวยวาดกราฟทั้งในสองมิติ และสามมิติ เป นจํานวนมาก และการกําหนดเสนโคงในระนาบ XY นิยมกําหนดเสนโคงในรูปสมการอิงตัวแปรเสริม
1. โค<งระนาบและสมการอิงตัวแปรเสริม
กําหนดให<พิกัด P(x, y) เปOนจุดบนเส<นโค<ง ซึ่งกําหนดด<วยฟwงกXชัน x = f (t) และ
y = g(t) แล<วสมการ x = f (t) และ y = g(t) จะถูกเรียกวTา สมการอิงตัวแปรเสริม (Parametric Equation) และ t เรียกวาT ตัวแปรเสริม (Parameter)
ตัวอยTางที่ 1 จงเขียนกราฟของสมการอิงตัวแปรเสริม x = 3 − 4t และ y = 2 + 5t ท กุ ค T า ข อ ง t
17
วิธีทํา จาก x = 3−4t จะได< t = !−#
""rZ ดังนั้น y = −2+5~j −j
y = 7−5x 4