Page 23 - E-Book Matematika..._Neat

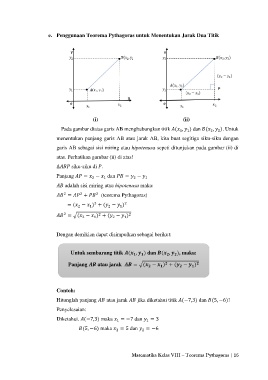
e. Penggunaan Teorema Pythagoras untuk Menentukan Jarak Dua Titik

(i) (ii)

Pada gambar diatas garis AB menghubungkan titik ( , ) dan ( , ). Untuk
1
2
1
2
menentukan panjang garis AB atau jarak AB, kita buat segitiga siku-siku dengan
garis AB sebagai sisi miring atau hipotenusa sepeti ditunjukan pada gambar (ii) di
atas. Perhatikan gambar (ii) di atas!
∆ siku-siku di .

Panjang = − dan = −
1
2
1
2
adalah sisi miring atau hipotenusa maka:
2
2
2
= + (teorema Pythagoras)
= ( − ) + ( − )
2
2
2
2
1
1
= √( − ) + ( − )
2
2
2
2
1
2
1

Dengan demikian dapat disimpulkan sebagai berikut:

Untuk sembarang titik ( , ) dan ( , ), maka:

Panjang atau jarak = √( − ) + ( − )

Contoh:
Hitunglah panjang atau jarak jika diketahui titik (−7,3) dan (5, −6)!
Penyelesaian:
Diketahui. (−7,3) maka = −7 dan = 3
1
1
(5, −6) maka = 5 dan = −6
2
2

Matematika Kelas VIII – Teorema Pythagoras | 16