Page 138 - chapter 1

138
ΚΕΦΑΛΑΙΟ 1 - Όρια - Συνέχεια Συνάρτησης

ΜΟΡΦΗ : f(g(x)),f(x)... διπλή ανισότητα
ΖΗΤΟΥΜΕΝΟ : ο τύπος ή τιμή της συνάρτησης f

AΝΤΙΜΕΤΩΠΙΣΗ
Aν η δοσμένη ανισοτητα είναι της μορφής Α Β Γ
● Λύνουμε την Α Β ως προς f(x) η f(g(x))
● Λύνουμε την Β Γ ως προς f(x) η f(g(x))
● Θέτουμε y = g(x) και λύνουμε ως προς χ και προκύπτει
χ = h(y)
● Θέτουμε στη δοσμένη σχέση οπου χ το h(y) και προκύπτει ο ΄
τύπος της f ως προς y, οπότε αλλάζοντας το y με χ ...
● Προκύπτει:
f(x) ≥ α και f(x) ≤ α, οπότε f(x) = α

ΠΑΡΑΔΕΙΓΜΑ
Για τη συνάρτηση f: ισχύει:
f(x) χ +χ f(x-1)+2χ, για κάθε χ
2

Να βρείτε το τύπο της σ υ νάρτησης f
ΛΥΣ Η

Eίναι για κάθε χ
f(x) χ +χ f(x-1)+2χ
2

● f(x) χ +χ, χ (1)
2

● χ +χ f(x-1)+2χ (2)
2
● Για y=χ-1~
χ = y+1 η (2) γίνεται
(y+1) +y+1 f(y+1-1)+
2
+2(y+1)`
y +2y+1+y+1 f(y)+
2
+2y+2 `
f(y) y +y, y
2
Άρα για χ όπου y
f(x) x +x, χ (3)
2
Από τις (1) και (2) προκύπτει
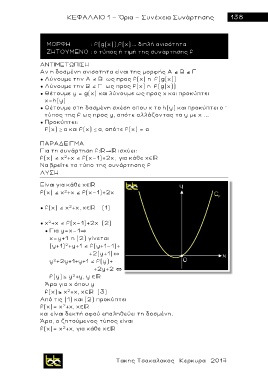
f(x)= x +x, χ
2
και είναι δεκτή αφού επαληθεύει τη δοσμένη.
Άρα, ο ζητούμενος τύπος είναι
f(x)= x +x, για κάθε χ
2

Τακης Τσακαλακος Κερκυρα 2017