Page 139 - chapter 1

139
ΚΕΦΑΛΑΙΟ 1 - Όρια - Συνέχεια Συνάρτησης

ΜΟΡΦΗ : f(xy)= f(x), f(y)...
x
ΖΗΤΟΥΜΕΝΟ : αποδειξη f y = ...

AΝΤΙΜΕΤΩΠΙΣΗ
● Θέτουμε στη δοσμένη σχέση , x = y = 1 .
Έτσι θα βρούμε τη τιμή f(1)
● Κρατούμε σταθερό τον x και θέτουμε στη δοσμένη σχέση
1 1
y = . Έτσι θα εμφανίσουμε την f(x), f(1) και f ...
x x
● Κρατούμε σταθερό τον x και θέτουμε στη δοσμένη σχέση ,

1 x
y = . Έτσι θα εμφανίσουμε την f .
y y

ΠΑΡΑΔΕΙΓΜΑ
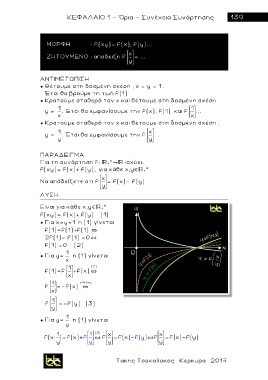
Για τη συνάρτηση f: +* ισχύει:
f(xy)= f(x)+ f(y), για κάθε χ,y +*

x
Να απόδείξετε οτι f = f(x)- f(y)
y

ΛΥΣ Η

Eίναι για κάθε χ , y +*
f(xy)= f(x)+ f(y) (1)
● Για x=y=1 η (1) γίνεται

f(1)=f(1)+f(1) `
2f(1)- f(1) =0`
f(1) =0 (2)
1
● Για y= η (1) γίνεται
x
1 (2)
f(1)=f +f(x) `
x
1 για χ=y
f =-f(x) `
x

1
f =-f(y) (3)
y

1
● Για y= η (1) γίνεται
y

1 1 (3 ) x x
f(x× )=f(x)+f ` f =f(x)-f(y) `f =f(x)-f(y)
y y y y

Τακης Τσακαλακος Κερκυρα 2017