Page 161 - chapter 1

161
ΚΕΦΑΛΑΙΟ 1 - Όρια - Συνέχεια Συνάρτησης

τότε
lim f(x) lim g(x)
x x 0 x x 0
παράδειγμα
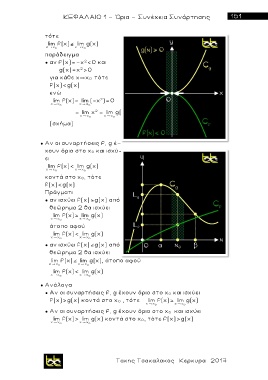
● αν f(x)=-χ <0 και
2
g(x)=χ >0
2
για κάθε χ x 0 τότε

f(x)<g(x)
ενώ
2
lim f(x)= lim (-χ ) 0
x x 0 x x 0

lim χ 2 lim g(x)
x x 0 x x 0
(σχήμα)

● Αν οι συναρτήσεις f, g έ-
χουν όριο στο χ 0 και ισχύ-
ε ι
lim f(x) lim g(x)
x x 0 x x 0
κοντά στο χ 0, τότε
f(x)<g(x)
Π ρ άγματι
● αν ισχύει f(x) g(x) από
θ ε ώρημα 2 θα ισχύει

lim f(x) lim g(x)
x x 0 x x 0
άτοπο αφού
lim f(x) lim g(x)
x x 0 x x 0
● αν ισχύει f(x) g(x) από
θ ε ώρημα 2 θα ισχύει
lim f(x) lim g(x), άτοπο αφού
x x 0 x x 0
lim f(x) lim g(x)
x x 0 x x 0
● Α ν άλογα
● Αν οι συναρτήσεις f, g έχουν όριο στο χ 0 και ισχύει
f(x)>g(x) κοντά στο χ 0 , τότε lim f(x) lim g(x)
x x 0 x x 0
● Αν οι συναρτήσεις f, g έχουν όριο στο χ 0 και ισχύει
lim f(x) lim g(x) κοντά στο χ 0, τότε f(x)>g(x)
x x 0 x x 0

Τακης Τσακαλακος Κερκυρα 2017