Page 163 - chapter 1

163
ΚΕΦΑΛΑΙΟ 1 - Όρια - Συνέχεια Συνάρτησης

έστω το πολυώνυμο P(x) α x +α ν -1 x ν -1 +... +α x+α , χ 0
ν
ν
0
1
lim P(x) lim [α x ν α x ν-1 +... +α x+α ]
x x 0 x x 0 ν ν-1 1 0
(1)
= lim (α x ) lim (α x ν-1 )+... + lim (α x)+ lim (α )
ν
x x 0 ν x x 0 ν-1 x x 0 1 x x 0 0
lim (x)+ lim (α )
α ν x x 0 ν ν - 1 x x 0 ν-1 )+... +α 1 x x 0 x x 0 0
lim (x ) α
lim (x
α ν x 0 ν α ν-1 x 0 ν-1 +... +α 1 x +α 0 Ρ(x )
0
0

● Όριο ρ η τ ή ς συνάρτησης
P(x) P(x )
lim = 0 με Q(x) 0 και χ 0
x x 0 Q(x) Q(x )
0
π ρ άγματι

P(x) lim P(x) P(x )
lim = x x 0 = 0
x x 0 Q(x) lim Q(x) Q(x )
x x 0 0

ΠΑΡΑΤΗΡΗΣΕΙΣ

● Το αντίστροφο του θεωρήματος 3 (εκτός της ιδιότητας 6)
δεν ισχύει, δηλαδή
μπορεί να ισχύει μία από τις πέντε πρώτες ιδιότητες και να
μην υπάρχουν απαραίτητα τα όρια των συναρτήσεων f και g.

ΠΑΡΑΔΕΙΓΜΑΤΑ

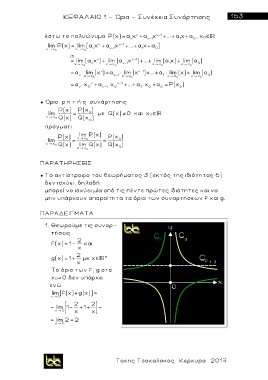
1. Θεωρούμε τις συναρ-

τήσεις
f(x)=1- 2 και
x
2
g(x)=1+ με χ *
x
Το όριο των f, g στο
χ 0=0 δεν υπάρχει
ενώ
lim[f(x)+g(x)]=
x 0
2 2
= lim 1- 1
x 0

= lim 2 2
x 0

Τακης Τσακαλακος Κερκυρα 2017