Page 283 - chapter 1

ΚΕΦΑΛΑΙΟ 1 - Όρια - Συνέχεια Συνάρτησης 283

Σ Υ Ν ΕΧΕΙΑ ΣΕ Δ Ι ΑΣΤΗΜΑ

ΟΡΙΣΜΟΣ

● Μια συνάρτηση f θα λέμε ότι είναι
συνεχής σε ένα ανοικτό δ ι άστημα (α,β)
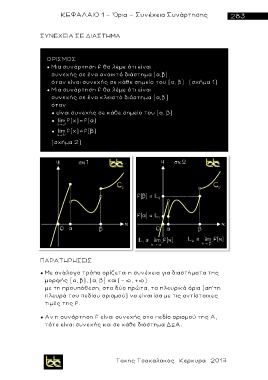
όταν είναι συνεχής σε κάθε σημείο του (α, β) (σχήμα 1)

● Μια συνάρτηση f θα λέμε ότι είναι
συνεχής σε ένα κλειστό δ ι άστημα [α,β]
όταν
● είναι συνεχής σε κάθε σημείο του (α, β)

● x lim f(x)=f(α)
lim f(x)=f(β)
● x
(σχήμα 2)

ΠΑΡΑΤΗΡΗΣΕΙΣ

● Με ανάλογο τρόπο ορίζεται η συνέχεια για διασ τ ήματα της

μορφής [α, β), (α, β] και (- , + )

με τη προυπόθεση, στα δύο πρώτα, τα πλευρικά όρια (απ'τη
πλευρά του πεδίου ορισμού) να είναι ίσα με τις αντίστοιχες

τιμές της f.

● Αν η συνάρτηση f είναι συνεχής στο πεδίο ορισμού της Α,

τότε είναι συνεχής και σε κάθε διάστημα Δ Α.

Τακης Τσακαλακος Κερκυρα 2017