Page 287 - chapter 1
P. 287
ΚΕΦΑΛΑΙΟ 1 - Όρια - Συνέχεια Συνάρτησης 287
χουν α,β Α με α<β τέτοια, ώστε f(α)<0 και f(β)>0
(όμοια αν α>β και f(α)>0 και f(β)<0)
Έτσι
● η f συνεχής στο [α, β] Α
● f(α) f(β)<0
Από θεώρημα Bolzano θα υπάρχει τουλάχιστον ένα
χ 0 (α, β) Α με f(χ 0)=0 που είναι άτοπο αφού f(x) 0 για
κάθε χ Α .
● Μια συνεχής συνάρτηση δ ι α τ η ρ ε ί π ρ ό σ η μ ο μεταξύ
δύο διαδοχικών ριζών της.
ΑΠΟΔΕΙΞΗ
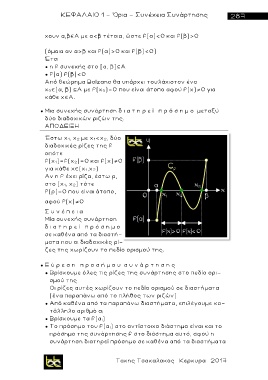
Έστω χ 1, χ 2 με χ 1<χ 2, δύο
διαδοχικές ρίζ ε ς της f
οπότ ε
f(χ 1)=f( χ 2)=0 και f(x) 0
για κάθε χ (χ 1,χ 2)
Αν η f έχει ρίζα, έστω ρ,
στο (χ 1, χ 2) τότε
f(ρ)=0 που είναι άτοπο,
αφού f(x) 0
Σ υ ν έ π ε ι α
Μία συνεχής συνάρτηση
δ ι α τ η ρ ε ί π ρ ό σ η μ ο
σε καθένα α π ό τα διασ τ ή-
ματα που οι διαδοχικές ρί-
ζες της χωρίζουν το πεδίο ορισμ ο ύ της.
● E ύ ρ ε σ η π ρ ο σ ή μ ο υ σ υ ν ά ρ τ η σ η ς
● Β ρ ίσκουμε όλες τις ρίζες της συνάρτησης στο πεδίο ορι-
σμού της
Οι ρίζες αυτές χωρίζουν το πεδίο ορισμού σε διασ τ ήματα
(ένα παραπάν ω α π ό το πλήθος των ριζών )
● Από καθένα α π ό τα παραπάνω διασ τ ήμ α τα, επιλέγουμε κα-
τάλληλο αριθμό α i
● Β ρ ίσκουμε τα f(α i)
● Το πρόσημο του f(α i) στο αντίστοιχο διάστημα είναι και το
π ρ όσημο της συνάρτησης f στο διάστημα αυτό, αφού η
συνάρτηση διατηρεί π ρ όσημο σε καθένα από τα δ ι ασ τ ήματα
Τακης Τσακαλακος Κερκυρα 2017