Page 290 - chapter 1

ΚΕΦΑΛΑΙΟ 1 - Όρια - Συνέχεια Συνάρτησης 290

ΠΑΡΑΔΕΙΓΜΑΤΑ

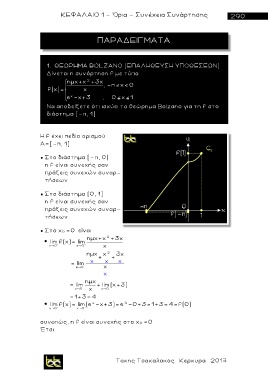
1. ΘΕΩΡΗΜΑ BOLZANO (ΕΠΑΛΗΘΕΥΣΗ ΥΠΟΘΕΣΕΩΝ)
Δίνεται η συνάρτηση f με τύπο
ημχ+x 2 +3x
f(x)= x , -π x< 0
x
e x+3 , 0 x 1
Να αποδείξετε ότι ισχύει το θεώρημα Bolzano για τη f στο
διάστημα [-π, 1]

H f έχει πεδίο ορισμού
Α=[-π, 1]

● Στο διάστημα [-π, 0)
η f είναι συνεχής σαν
π ρ άξεις συνεχών συναρ-
τήσεων

● Στο διάστημα (0, 1]
η f είναι συνεχής σαν
π ρ άξεις συνεχών συναρ-
τήσεων

● Στο x 0 =0 είναι
lim f(x)= lim ημx+x 2 +3x
x 0 x 0 x
ημx + x 2 + 3x

= lim x x x
x 0 x
x
ημx
= lim + lim(x+3)
x 0 x x 0
= 1+3= 4
lim f(x)= lim(e -x+3)=e -0+3=1+3=4=f(0)
x
0
x 0 x 0

συνεπώς, η f είναι συνεχής στο x 0 =0
Έτσι

Τακης Τσακαλακος Κερκυρα 2017