Page 285 - chapter 1

ΚΕΦΑΛΑΙΟ 1 - Όρια - Συνέχεια Συνάρτησης 285

ΠΑΡΑΤΗΡΗΣΕΙΣ

● Εναλλακτικά, το συμπέρασμα του θεωρήματος Bolzano
μπορεί να είναι:
" ... η γραφική παράσταση της συνάρτησης f τέμνει τον

άξονα χ'χ σε ένα τουλάχιστον σημείο με τετμημένη

χ 0 (α, β)"
● Το θεώρημα Βolzano εξασφαλίζει την ύ π α ρ ξ η ριζών
της f στο ανοικτό διάστημα (α, β) αλλά δεν δίνει πληροφο-
ρίες για το πλήθος των ριζών
● Αν όμως επιπλέον η f είναι γνησίως μόνοτονη στο [α, β],

τότε θα έχει μ ο ν α δ ι κ ή ρίζα στο (α, β )
● Το θεώρημα Βolzano εξασφαλίζει την ύ π α ρ ξ η ρίζας στο

ανοικτό διάστημα (α, β) αλλά δεν προσδιορίζει ποιά είναι αυτή
● Ισοδύναμες εκφράσεις

"... υπάρχει τουλάχιστον μια λύση της εξίσωσης f(x) = 0 ..."
"... υπάρχει τουλάχιστον μια ρίζα της συνάρτησης f ..."
" ... η γραφική παράσταση της συνάρτησης f τέμνει τον άξο-

να χ'χ σε ένα τουλάχιστον σημείο με τετμημένη χ 0 (α, β)... "
● Το αντίστροφο του θεωρήματος Βolzano δ ε ν ισχύει

ΠΑΡΑΔΕΙΓΜΑΤΑ

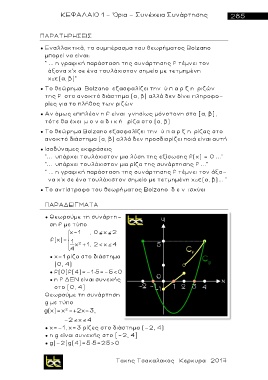
● Θεωρούμε τη συνάρτη-
ση f με τύπ ο
x-1 , 0 x 2
f(x)= 1 2

4 x +1, 2< x 4
● x=1 ρίζα στο διάστημα
(0, 4)
● f(0)f(4)=-1 5=-5<0
● η f ΔΕΝ είναι συνεχής
στο [0, 4]

Θεωρούμε τη συνάρτηση
g με τύπ ο
g(x)= x -+2x-3,
2

-2 x 4
● x=-1, χ=3 ρίζες στο διάστημα (-2, 4)
● η g είναι συνεχής στο [-2, 4]
● g(-2)g(4)=5 5=25>0

Τακης Τσακαλακος Κερκυρα 2017