Page 296 - chapter 1

ΚΕΦΑΛΑΙΟ 1 - Όρια - Συνέχεια Συνάρτησης 296

6. ΘΕΩΡΗΜΑ BOLZANO (ΑΝΟΙΚΤΟ ΑΚΡΟ ± )
Έστω η συνάρτηση f με τύπ ο
1
x
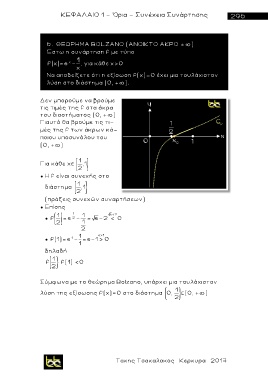
f(x) =e - x , για κάθε χ>0
Να αποδείξετε ότι η εξίσωση f(χ)=0 έχει μια τουλάχιστον
λύση στο διάστημα (0, + ).

Δεν μπορούμε να βρούμε
τις τιμές της f στα άκρα
του διασ τ ήματος (0, + )
Γιαυ τ ό θα βρούμε τις τι-
μές της f των άκρων κά-
ποιου υποσυνόλου του
(0, + )

1
Για κάθε χ ,1
2
● Η f είναι συνεχής στο
1
διάστημα ,1
2

(π ρ άξεις συνεχών συναρτήσεων)
● Επίσης

1 1 1 e < 2
● f = e 2 - = e-2 < 0
2 1
2
1 e > 1
● f(1)= e - = e-1 > 0
1
1
δηλαδή

1
f f(1) <0
2

Σύμφωνα με το θεώρημα Bolzano, υπάρχει μια τουλάχιστον
1
λύση της εξίσωσης f(x)=0 στο διάστημα 0, (0, + )
2

Τακης Τσακαλακος Κερκυρα 2017