Page 3 - FUNGSI KUADRAT KE 5

3.4.2 Mengidentifikasi sumbu simetri dari grafik fungsi kuadrat f(x) dengan memperhatikan nilai dari
koefisien x2 dan x

Contoh
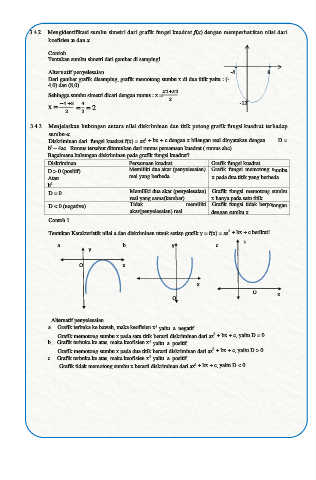
Tentukan sumbu simetri dari gambar di samping!

Alternatif penyelesaian -4 8
Dari gambar grafik disamping, grafik memotong sumbu x di dua titik yaitu : (-
4,0) dan (8,0).
1+ 2
Sehingga sumbu simetri dicari dengan rumus : x =
2 -12
4
x = −4 +8 = = 2
2 2

3.4.3 Menjelaskan hubungan antara nilai diskriminan dan titik potong grafik fungsi kuadrat terhadap
sumbu-x.
Diskriminan dari fungsi kuadrat f(x) = ax + bx + c dengan x bilangan real dinyatakan dengan D =
2
b – 4ac . Rumus tersebut diturunkan dari rumus persamaan kuadrat ( rumus abc).
2
Bagaimana hubungan diskriminan pada grafik fungsi kuadrat?
Diskriminan Persamaan kuadrat Grafik fungsi kuadrat
D > 0 (positif) Memiliki dua akar (penyelesaian) Grafik fungsi memotong sumbu
Atau real yang berbeda x pada dua titik yang berbeda
2
b
D = 0 Memiliki dua akar (penyelesaian) Grafik fungsi memotong sumbu
real yang sama(kembar) x hanya pada satu titik
D < 0 (negative) Tidak memiliki Grafik fungsi tidak berpotongan
akar(penyelesaian) real dengan sumbu x
Contoh 1

2
Tentukan Karakteristik nilai a dan diskriminan utnuk setiap grafik y = f(x) = ax + bx + c berikut!
y
a. b. y c
y

O x

x
O
O x

Alternatif penyelesaian
2
a. Grafik terbuka ke bawah, maka keofisien x yaitu a negatif.
Grafik memotong sumbu x pada satu titik berarti diskriminan dari ax + bx + c, yaitu D = 0
2
b. Grafik terbuka ke atas, maka keofisien x yaitu a positif.
2
Grafik memotong sumbu x pada dua titik berarti diskriminan dari ax + bx + c, yaitu D > 0
2
2
c. Grafik terbuka ke atas, maka keofisien x yaitu a positif.
2
Grafik tidak memotong sumbu x berarti diskriminan dari ax + bx + c, yaitu D < 0