Page 175 - [Uma_Sekaran]_Research_methods_for_business__a_sk(BookZZ.org)

TYPES OF EXPERIMENTAL DESIGNS AND INTERNAL VALIDITY 159

not measure the true cause-and-effect relationship. This is so because there is
no comparison between groups, nor any recording of the status of the depen-
dent variable as it was prior to the experimental treatment and how it changed
after the treatment. In the absence of such control, the study is of no scientific
value in determining cause-and-effect relationships. Hence, such a design is
referred to as a quasi-experimental design. The following two are quasi-exper-
imental designs.

Pretest and Posttest Experimental Group Design
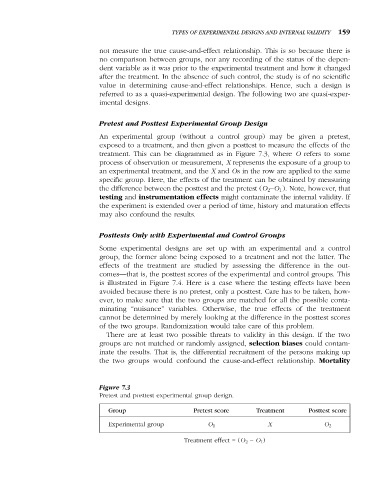
An experimental group (without a control group) may be given a pretest,
exposed to a treatment, and then given a posttest to measure the effects of the
treatment. This can be diagrammed as in Figure 7.3, where O refers to some
process of observation or measurement, X represents the exposure of a group to
an experimental treatment, and the X and Os in the row are applied to the same
specific group. Here, the effects of the treatment can be obtained by measuring
the difference between the posttest and the pretest (O 2 –O 1 ). Note, however, that
testing and instrumentation effects might contaminate the internal validity. If
the experiment is extended over a period of time, history and maturation effects
may also confound the results.

Posttests Only with Experimental and Control Groups
Some experimental designs are set up with an experimental and a control
group, the former alone being exposed to a treatment and not the latter. The
effects of the treatment are studied by assessing the difference in the out-
comes—that is, the posttest scores of the experimental and control groups. This
is illustrated in Figure 7.4. Here is a case where the testing effects have been
avoided because there is no pretest, only a posttest. Care has to be taken, how-
ever, to make sure that the two groups are matched for all the possible conta-
minating “nuisance” variables. Otherwise, the true effects of the treatment
cannot be determined by merely looking at the difference in the posttest scores
of the two groups. Randomization would take care of this problem.
There are at least two possible threats to validity in this design. If the two
groups are not matched or randomly assigned, selection biases could contam-
inate the results. That is, the differential recruitment of the persons making up
the two groups would confound the cause-and-effect relationship. Mortality

Figure 7.3
Pretest and posttest experimental group design.

Group Pretest score Treatment Posttest score
Experimental group O 1 X O 2

Treatment effect = (O 2 – O 1 )