Page 268 - Six Sigma Advanced Tools for Black Belts and Master Black Belts

OTE/SPH
OTE/SPH
3:5
Char Count= 0
JWBK119-16
August 31, 2006
Robust Design 253
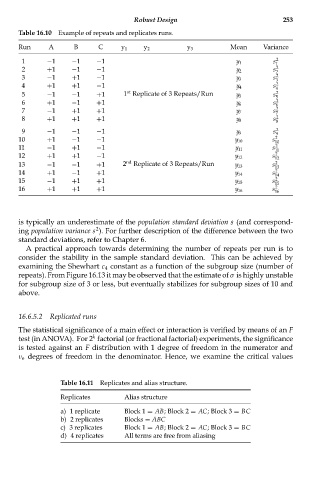
Table 16.10 Example of repeats and replicates runs.
Run A B C y 1 y 2 y 3 Mean Variance
1 −1 −1 −1 y 1 s 1 2
2 +1 −1 −1 s 2
y 2
2
3 −1 +1 −1 s 2
y 3
3
4 +1 +1 −1 s 2
y 4
4
st
5 −1 −1 +1 1 Replicate of 3 Repeats/Run s 2
y 5
5
6 +1 −1 +1 s 2
y 6
6
7 −1 +1 +1 s 2
y 7
7
8 +1 +1 +1 s 2
y 8
8
9 −1 −1 −1 s 2
y 9
9
10 +1 −1 −1 s 2
y 10
10
11 −1 +1 −1 s 2
y 11
11
2
12 +1 +1 −1 y 12 s 12
2
13 −1 −1 +1 2 nd Replicate of 3 Repeats/Run y 13 s 13
2
14 +1 −1 +1 y 14 s 14
2
15 −1 +1 +1 y 15 s 15
2
16 +1 +1 +1 y 16 s 16
is typically an underestimate of the population standard deviation s (and correspond-
2
ing population variance s ). For further description of the difference between the two
standard deviations, refer to Chapter 6.
A practical approach towards determining the number of repeats per run is to
consider the stability in the sample standard deviation. This can be achieved by
examining the Shewhart c 4 constant as a function of the subgroup size (number of
repeats). From Figure 16.13 it may be observed that the estimate of σ is highly unstable
for subgroup size of 3 or less, but eventually stabilizes for subgroup sizes of 10 and
above.
16.6.5.2 Replicated runs
The statistical significance of a main effect or interaction is verified by means of an F
k
test (in ANOVA). For 2 factorial (or fractional factorial) experiments, the significance
is tested against an F distribution with 1 degree of freedom in the numerator and
ν e degrees of freedom in the denominator. Hence, we examine the critical values
Table 16.11 Replicates and alias structure.
Replicates Alias structure
a) 1 replicate Block 1 = AB; Block 2 = AC; Block 3 = BC
b) 2 replicates Blocks = ABC
c) 3 replicates Block 1 = AB; Block 2 = AC; Block 3 = BC
d) 4 replicates All terms are free from aliasing