Page 38 - Mathematics of Business and Finance

18 Chapter 1 | Review of Basic Arithmetic

Solution Method 2
continued
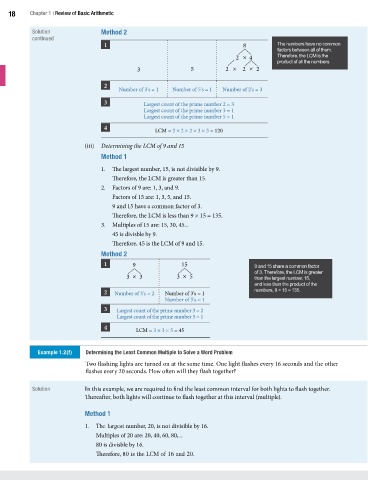
1 8 The numbers have no common
factors between all of them.
2 × 4 Therefore, the LCM is the
product of all the numbers.
3 5 2 × 2 × 2

2
Number of 3's = 1 Number of 5's = 1 Number of 2's = 3

3 Largest count of the prime number 2 = 3
Largest count of the prime number 3 = 1
Largest count of the prime number 5 = 1
4 LCM = 2 × 2 × 2 × 3 × 5 = 120

(iii) Determining the LCM of 9 and 15

Method 1
1. The largest number, 15, is not divisible by 9.
Therefore, the LCM is greater than 15.
2. Factors of 9 are: 1, 3, and 9.
Factors of 15 are: 1, 3, 5, and 15.
9 and 15 have a common factor of 3.
Therefore, the LCM is less than 9 × 15 = 135.
3. Multiples of 15 are: 15, 30, 45...
45 is divisble by 9.
Therefore, 45 is the LCM of 9 and 15.
Method 2
1 9 15 9 and 15 share a common factor
of 3. Therefore, the LCM is greater
3 × 3 3 × 5 than the largest number, 15,
and less than the product of the
2 Number of 3's = 2 Number of 3's = 1 numbers, 9 × 15 = 135.
Number of 5's = 1
3 Largest count of the prime number 3 = 2
Largest count of the prime number 5 = 1
4 LCM = 3 × 3 × 5 = 45

Example 1.2(f) Determining the Least Common Multiple to Solve a Word Problem
Two flashing lights are turned on at the same time. One light flashes every 16 seconds and the other
flashes every 20 seconds. How often will they flash together?

Solution In this example, we are required to find the least common interval for both lights to flash together.
Thereafter, both lights will continue to flash together at this interval (multiple).

Method 1

1. The largest number, 20, is not divisible by 16.
Multiples of 20 are: 20, 40, 60, 80,...
80 is divisble by 16.
Therefore, 80 is the LCM of 16 and 20.