Page 37 - Mathematics of Business and Finance

Chapter 1 | Review of Basic Arithmetic 17

For example, in finding the LCM of 3, 5, and 10, the largest number 10 is not divisible by 3, and 5
Example 1.2(a) Identifying Prime Numbers and Composite Numbers and 10 have a common factor of 5. Multiples of 10 are 10, 20, 30, 40, etc. 30 is divisible by both 3
(i) Identify all the prime numbers less than 25. and 5. Therefore, the LCM of 3, 5, and 10 is 30.
(ii) Identify all the composite numbers less than 25. Method 2

Step 1: Find the prime factors of each of the numbers using a factor tree and list the different prime
Solution (i) All the prime numbers less than 25 are: 2, 3, 5, 7, 11, 13, 17, 19, and 23.
numbers.
(ii) All the composite numbers less than 25 are: 4, 6, 8, 9, 10, 12, 14, 15, 16, 18, 20, 21, 22, and 24.
Step 2: Count the number of times each different prime number appears in each of the factorizations.
Example 1.2(b) Determining Factors of Prime Numbers Step 3: Find the largest of these counts for each prime number.
Determine all the factors of 13. Step 4: List each prime number as many times as you counted it in Step 3. The LCM is the product of
all the prime numbers listed.
Solution 1 and 13 are the only factors of 13. 1 13
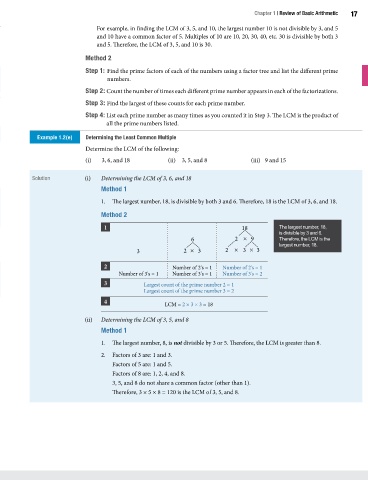
Example 1.2(e) Determining the Least Common Multiple
Determine the LCM of the following:
Example 1.2(c) Determining All Factors of Composite Numbers
(i) 3, 6, and 18 (ii) 3, 5, and 8 (iii) 9 and 15
Determine all the factors of:
(i) 18 (ii) 20 Solution (i) Determining the LCM of 3, 6, and 18
Method 1
Solution (i) The factors of 18 are: 1, 2, 3, 6, 9, and 18. 1 2 3 6 9 18
1. The largest number, 18, is divisible by both 3 and 6. Therefore, 18 is the LCM of 3, 6, and 18.
(ii) The factors of 20 are: 1, 2, 4, 5, 10, and 20. 1 2 4 5 10 20 Method 2

1 18 The largest number, 18,
is divisible by 3 and 6.
Example 1.2(d) Determining Prime Factors of Composite Numbers 6 2 × 9 Therefore, the LCM is the
largest number, 18.
Determine the prime factors of 24. 3 2 × 3 2 × 3 × 3

Solution All the factors of 24 are: 1, 2, 3, 4, 6, 8, 12, and 24. 1 2 3 4 6 8 12 24 2 Number of 2's = 1 Number of 2's = 1
Number of 3's = 1 Number of 3's = 1 Number of 3's = 2
In the above factors, only 2 and 3 are prime numbers. 3 Largest count of the prime number 2 = 1
Therefore, the prime factors of 24 are: 2 and 3. Largest count of the prime number 3 = 2
4 LCM = 2 × 3 × 3 = 18
Least or Lowest Common Multiple (LCM)

The Least Common Multiple (LCM) of two or more whole numbers is the smallest multiple that is (ii) Determining the LCM of 3, 5, and 8
common to those numbers. The LCM can be determined using one of the following methods: Method 1
Method 1 1. The largest number, 8, is not divisible by 3 or 5. Therefore, the LCM is greater than 8.

1. First, select the largest number and check to see if it is divisible by all the other numbers. If it 2. Factors of 3 are: 1 and 3.
divides, then the largest number is the LCM. Factors of 5 are: 1 and 5.

For example, in finding the LCM of 2, 3, and 12, the largest number 12 is divisible by the other Factors of 8 are: 1, 2, 4, and 8.
numbers 2 and 3. Therefore, the LCM of 2, 3, and 12 is 12. 3, 5, and 8 do not share a common factor (other than 1).
2. If none of the numbers have a common factor, then the LCM of the numbers is the product of all Therefore, 3 × 5 × 8 = 120 is the LCM of 3, 5, and 8.
the numbers.
For example, in finding the LCM of 2, 5, and 7, none of these numbers have a common factor.
Therefore, the LCM of 2, 5, and 7 is 2 × 5 × 7 = 70.
3. If the largest number is not divisible by the other numbers and there is a common factor between
some of the numbers, then find a multiple of the largest number that is divisible by all the other
numbers.