Page 3 - Modul_matematika_trigonometri_Neat

www.matematika-pas.blogspot.com 2

E-learning matematika, GRATIS

II. NILAI PERBANDINGAN TRIGONOMETRI DARI SUATU SUDUT
Trigonometri terdiri dari sinus(sin), cosinus(cos), tangens(tan),
cotangens(cot), secan(sec), dan cosecan(cosec). Trigonometri merupakan nilai
perbandingan yang dapat didefinisikan pada koordinat Cartesius atau segitiga
siku-siku.
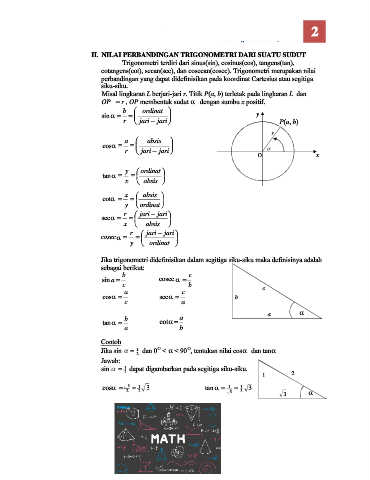
Misal lingkaran L berjari-jari r. Titik P(a, b) terletak pada lingkaran L dan
OP = r , OP membentuk sudut α dengan sumbu x positif.
b ⎛ ordinat ⎞
sin α = = ⎜ ⎜ ⎟ y
⎟
r ⎝ jari − jari ⎠ P(a, b)
r
a ⎛ absis ⎞
cos α = = ⎜ ⎜ ⎟ ⎟ α
r ⎝ jari − jari ⎠ O x

⎜
tan α = y = ⎛ ordinat ⎞ ⎟
x ⎝ absis ⎠

x ⎛ absis ⎞
cot α = = ⎜ ⎟
y ⎝ ordinat ⎠
r ⎛ jari − jari ⎞
sec α = = ⎜ ⎟
x ⎝ absis ⎠
r ⎛ jari − jari ⎞
cosecα = = ⎜ ⎟
y ⎝ ordinat ⎠

Jika trigonometri didefinisikan dalam segitiga siku-siku maka definisinya adalah
sebagai berikut:
b c
sin a = cosecα =
c b c
a c
cos α = sec α = b
c a
α
b a a
tan α = cot α =
a b

Contoh
O
O
Jika sin α = dan 0 < α < 90 , tentukan nilai cosα dan tanα
1
2
Jawab:
sin α = dapat digambarkan pada segitiga siku-siku.
1
2
1 2
α
cos = 3 = 1 3 tanα = 1 = 1 3
2 2 3 3 3 α

MGMP Matematika SMK kota Pasuruan