Page 101 - Maxwell House

NEOCLASSICAL THEORY OF INTERACTION 81

15 , the domains
spinning in the same direction . In response to an external magnetizing field
and their magnetic moments are partially aligned in parallel with and grow at the expense
of unaligned domains (see Figure 2.6.2b). As far as the strength of increases, the magnetic
moment reaches the maximum when all domains merge into a single domain shown in Figure
2.6.2c meaning that material is fully magnetized. Explicitly, due to absence of extra domains to
be aligned, the moment practically stops growing beyond this point reaching the state of
magnetic saturation.

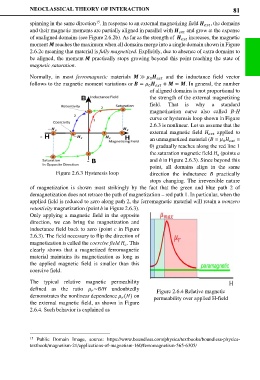
Normally, in most ferromagnetic materials ≫ and the inductance field vector
0
follows to the magnetic moment variations or = + ≈ . In general, the number
0
of aligned domains is not proportional to
the strength of the external magnetizing
field. That is why a standard
magnetization curve also called B-H
curve or hysteresis loop shown in Figure
2.6.3 is nonlinear. Let us assume that the

external magnetic field applied to
an unmagnetized material (B = =
0
0) gradually reaches along the red line 1
the saturation magnetic field (points a

and h in Figure 2.6.3). Since beyond this
point, all domains align in the same
Figure 2.6.3 Hysteresis loop direction the inductance B practically
stops changing. The irreversible nature
of magnetization is shown most strikingly by the fact that the green and blue path 2 of
demagnetization does not retrace the path of magnetization – red path 1. In particular, when the
applied field is reduced to zero along path 2, the ferromagnetic material will retain a nonzero
retentivity magnetization (point b in Figure 2.6.3).
Only applying a magnetic field in the opposite
direction, we can bring the magnetization and
inductance field back to zero (point c in Figure
2.6.3). The field necessary to flip the direction of
magnetization is called the coercive field . This

clearly shows that a magnetized ferromagnetic
material maintains its magnetization as long as
the applied magnetic field is smaller than this
coercive field.
The typical relative magnetic permeability
defined as the ratio ~B/H undoubtedly Figure 2.6.4 Relative magnetic

demonstrates the nonlinear dependence () on permeability over applied H-field

the external magnetic field, as shown in Figure
2.6.4. Such behavior is explained as

15 Public Domain Image, source: https://www.boundless.com/physics/textbooks/boundless-physics-
textbook/magnetism-21/applications-of-magnetism-160/ferromagnetism-565-6305/