Page 103 - Maxwell House

NEOCLASSICAL THEORY OF INTERACTION 83

If so, plenty of domain magnetic moments cannot keep up with the oscillating magnetic field
staying unaligned. As such, the orientation
magnetic polarization diminishes drastically as
the external magnetic field frequency is even
slightly above zero. Consequently, the
magnetic permeability drops incredibly fast as
frequency increases. Figure 2.6.5 illustrates
this effect for several magnetic alloys with
ultra-high magnetic permeability [23]. The
abbreviation “wt.” stands for the word
“weight.”
Figure 2.6.5 Relative magnetic
permeability over frequency 2.6.4 Ferrimagnetic and Ferrites
As noted above in the introduction to this
section, ferrimagnetism essentially is the same but a weaker form of ferromagnetism.
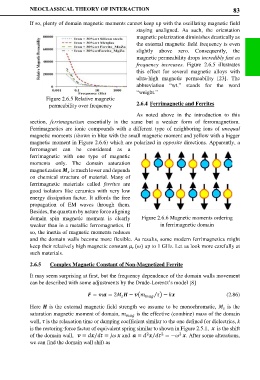
Ferrimagnetics are ionic compounds with a different type of neighboring ions of unequal
magnetic moments (shown in blue with the small magnetic moment and yellow with a bigger
magnetic moment in Figure 2.6.6) which are polarized in opposite directions. Apparently, a
ferromagnet can be considered as a
ferrimagnetic with one type of magnetic
moments only. The domain saturation
magnetization is much lower and depends

on chemical structure of material. Many of
ferrimagnetic materials called ferrites are
good isolators like ceramics with very low
energy dissipation factor. It affords the free
propagation of EM waves through them.
Besides, the quantum by nature force aligning
domain spin magnetic moment is clearly Figure 2.6.6 Magnetic moments ordering
weaker than in a metallic ferromagnetics. If in ferrimagnetic domain
so, the inertia of magnetic moments reduces
and the domain walls become more flexible. As results, some modern ferrimagnetics might
keep their relatively high magnetic constant () up to 1 GHz. Let us look more carefully at

such materials.
2.6.5 Complex Magnetic Constant of Non-Magnetized Ferrite
It may seem surprising at first, but the frequency dependence of the domain walls movement
can be described with some adjustments by the Drude-Lorentz’s model [8]

= = 2 − � ⁄ � − (2.86)

Here is the external magnetic field strength we assume to be monochromatic, is the

saturation magnetic moment of domain, is the effective (combine) mass of the domain
wall, is the relaxation time or damping coefficient similar to the one defined for dielectrics, k
is the restoring-force factor of equivalent spring similar to shown in Figure 2.5.1, is the shift
of the domain wall, = = and = = − . After some alterations,
2
2
2
⁄
⁄
we can find the domain wall shift as