Page 105 - Maxwell House

NEOCLASSICAL THEORY OF INTERACTION 85

absence of an external electric field. The spontaneous electric polarization of single-domain
materials usually lies within the range 10 to gigantic 1 C/m . They are reoriented in parallel
−3
2
by an external electric field larger than the coercive field the same way as the ferrimagnetic

domains align in a magnetic field. Both types of materials exhibit a hysteresis shown in Figure
2.6.3 and a residual polarization/magnetization, respectively even after the driving
electric/magnetic force has been removed. In the
presence of weak electric field, the polarization
vector P is practically proportional to electric field
E as in an ordinary dielectric. Equally, in stronger
electric field the domains polarized in the direction
of applied field expands and the polarization vector
P rapidly increases. As soon as all domains are
oriented in the direction of the applied field the
polarization vector P reaches the saturation. As a
result, the ferroelectrics demonstrate the strong
nonlinear dielectric response to an applied electric
field similar to the shown in Figure 2.6.7. The main
difference is that all ferroelectric materials are
generally piezoelectric, but not all piezoelectric
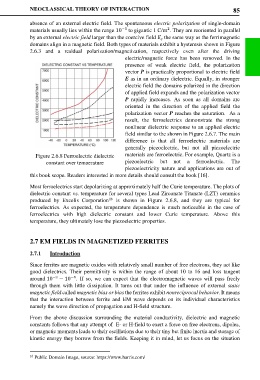
Figure 2.6.8 Ferroelectric dielectric materials are ferroelectric. For example, Quartz is a
constant over temperature piezoelectric but not a ferroelectric. The
piezoelectricity nature and applications are out of
this book scope. Readers interested in more details should consult the book [16].

Most ferroelectrics start depolarizing at approximately half the Curie temperature. The plots of
dielectric constant vs. temperature for several types Lead Zirconate Titanate (LZT) ceramics
produced by Excelis Corporation is shown in Figure 2.6.8, and they are typical for
16
ferroelectrics. As expected, the temperature dependence is much noticeable in the case of
ferroelectrics with high dielectric constant and lower Curie temperature. Above this
temperature, they ultimately lose the piezoelectric properties.

2.7 EM FIELDS IN MAGNETIZED FERRITES

2.7.1 Introduction

Since ferrites are magnetic oxides with relatively small number of free electrons, they act like
good dielectrics. Their permittivity is within the range of about 10 to 16 and loss tangent
−4
around 10 −3 − 10 . If so, we can expect that the electromagnetic waves will pass freely
through them with little dissipation. It turns out that under the influence of external static
magnetic field called magnetic bias or bias the ferrites exhibit nonreciprocal behavior. It means
that the interaction between ferrite and EM wave depends on its individual characteristics
namely the wave direction of propagation and H-field structure.
From the above discussion surrounding the material conductivity, dielectric and magnetic
constants follows that any attempt of E- or H-field to exert a force on free electrons, dipoles,
or magnetic moments leads to their oscillations due to their tiny but finite inertia and storage of
kinetic energy they borrow from the fields. Keeping it in mind, let us focus on the situation

16 Public Domain Image, source: https://www.harris.com/