Page 104 - Maxwell House

84 Chapter 2

2

= 0 (2.87)
2
2
− +/
0
The induced by the shifted wall magnetic moment is proportional to the shift of the domain
wall. Therefore, the extra magnetic moment appeared by the wall shift is = 2 . If so

(check 1.90),
2

= + = �1 + � (2.88)
0
0
2
2
− +/
0
⁄
⁄
Here = �2 ( ) is the magnetic plasma frequency and = � is the

0

0
resonance frequency of the domain wall oscillation. Explicitly, the factor in the parenthesis of
(2.88) is the relative complex magnetic constant
2

′′
′
() = () − () = 1 + (2.89)
2 2
− +/
0
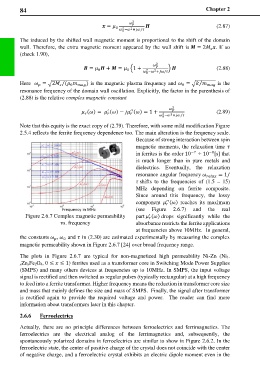
Note that this equity is the exact copy of (2.79). Therefore, with some mild modification Figure
2.5.4 reflects the ferrite frequency dependence too. The main alteration is the frequency scale.
Because of strong interaction between spin
magnetic moments, the relaxation time
−8
in ferrites is the order 10 −7 ÷ 10 [s] that
is much longer than in pure metals and
dielectrics. Eventually, the relaxation
resonance angular frequency = 1/
shifts to the frequencies of (1.5 – 15)
MHz depending on ferrite composite.
Since around this frequency, the lossy
component () reaches its maximum
′′

(see Figure 2.6.7) and the real
Figure 2.6.7 Complex magnetic permeability part () drops significantly while the
′

vs. frequency absorbance restricts the ferrite applications
at frequencies above 10MHz. In general,
the constants , and in (2.30) are estimated experimentally by measuring the complex

0
magnetic permeability shown in Figure 2.6.7 [24] over broad frequency range.
The plots in Figure 2.6.7 are typical for non-magnetized high permeability Ni-Zn (Ni1-
xZnxFe2O4, 0 ≤ ≤ 1) ferrites used as a transformer core in Switching Mode Power Supplies
(SMPS) and many others devices at frequencies up to 10MHz. In SMPS, the input voltage
signal is rectified and then switched as regular pulses (typically rectangular) at a high frequency
to feed into a ferrite transformer. Higher frequency means the reduction in transformer core size
and mass that mainly defines the size and mass of SMPS. Finally, the signal after transformer
is rectified again to provide the required voltage and power. The reader can find more
information about transformers later in this chapter.
2.6.6 Ferroelectrics
Actually, there are no principle differences between ferroelectrics and ferrimagnetics. The
ferroelectrics are the electrical analog of the ferrimagnetics and, subsequently, the
spontaneously polarized domains in ferroelectrics are similar to show in Figure 2.6.2. In the
ferroelectric state, the center of positive charge of the crystal does not coincide with the center
of negative charge, and a ferroelectric crystal exhibits an electric dipole moment even in the