Page 109 - Maxwell House

NEOCLASSICAL THEORY OF INTERACTION 89

In its turn, the moving electrons interact with surrounding them other material particles giving
them part of their energy too. Therefore, the part of alternative field energy is lost forever. To
account this damping effect let compare (2.97) with (2.79) and (2.89). They are almost the same
except the term /. Unfortunately, the simple Drude-Lorentz’s model with single spring does
not properly reflect the complexity of spin precessing but the adjustment is very mild and
reduced to the replacement → + /
0
0
′ ′′ � (2.98)
= − = �1 −
0
±
±
±
0 ∓+/
The constant [s] keeps
its meaning of the
damping factor and is
around several tens in
high quality low-loss
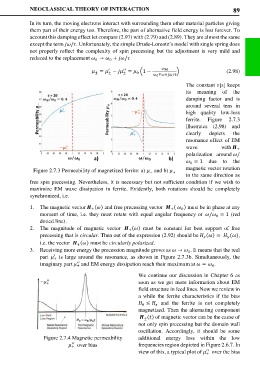
ferrite. Figure 2.7.3
illustrates (2.98) and
clearly depicts the
resonance effect of EM
wave with
+
polarization around /
= 1 due to the
0
Figure 2.7.3 Permeability of magnetized ferrite: a) and b) magnetic vector rotation
+
in the same direction as
−
free spin precessing. Nevertheless, it is necessary but not sufficient condition if we wish to
maximize EM wave dissipation in ferrite. Evidently, both rotations should be completely
synchronized, i.e.

1. The magnetic vector () and free precessing vector ( ) must be in phase at any
0
+
+
moment of time, i.e. they must rotate with equal angular frequency or / = 1 (red
0
dotted line).
2. The magnitude of magnetic vector () must be constant for best support of free
+
precessing that is circular. Then out of the expression (2.92) should be () = (),

i.e. the vector () must be circularly polarized.
+
3. Receiving more energy the precession magnitude grows as → . It means that the real
0
part is large around the resonance, as shown in Figure 2.7.3b. Simultaneously, the
′
+
imaginary part and EM energy dissipation reach their maximum at = .
′′
0
+
We continue our discussion in Chapter 6 as
soon as we get more information about EM
field structure in feed lines. Now we review in
a while the ferrite characteristics if the bias
≤ and the ferrite is not completely
0

magnetized. Then the alternating component
() of magnetic vector can be the cause of
±
not only spin precessing but the domain wall
oscillation. Accordingly, it should be some
Figure 2.7.4 Magnetic permeability additional energy loss within the low
over bias frequencies region depicted in Figure 2.6.7. In
′′
+
view of this, a typical plot of over the bias
′′
+