Page 113 - Maxwell House

NEOCLASSICAL THEORY OF INTERACTION 93

2.8.2 Negative Permittivity and Permeability

Let us look back at Drude-
Lorentz’s model for electric and
magnetic polarization effects
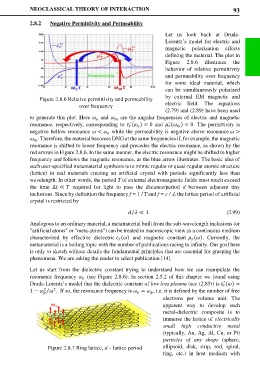
defining the material. The plot in
Figure 2.8.6 illustrates the
behavior of relative permittivity
and permeability over frequency
for some ideal material, which
can be simultaneously polarized
Figure 2.8.6 Relative permittivity and permeability by external EM magnetic and
over frequency electric field. The equations
(2.79) and (2.89) have been used
to generate this plot. Here and are the angular frequencies of electric and magnetic

resonance, respectively, corresponding to ( ) = 0 and ( ) = 0. The permittivity is
′
′

negative bellow resonance < while the permeability is negative above resonance >

. Therefore, the material becomes DNG at the same frequencies if, for example, the magnetic

resonance is shifted to lower frequency and precedes the electric resonance, as shown by the
red arrows in Figure 2.8.6. In the same manner, the electric resonance might be shifted to higher
frequency and follows the magnetic resonance, as the blue arrow illustrates. The basic idea of
such user-specified metamaterial synthesis is to mimic regular or quasi-regular atomic structure
(lattice) in real materials creating an artificial crystal with periods significantly less than
wavelength. In other words, the period T of external electromagnetic fields must much exceed
the time ∆ ≪ required for light to pass the distance/period d between adjacent tiny
inclusions. Since by definition the frequency f = 1 / T and f = c / , the lattice period of artificial
crystal is restricted by
≪ 1 (2.99)
⁄
Analogous to an ordinary material, a metamaterial built from the sub-wavelength inclusions (or
"artificial atoms" or "meta-atoms") can be treated in macroscopic view as a continuous medium
characterized by effective dielectric () and magnetic constant (). Currently, the

metamaterial is a boiling topic with the number of publications racing to infinity. Our goal here
is only to sketch without details the fundamental principles that are essential for grasping the
phenomena. We are asking the reader to select publication [14].
Let us start from the dielectric constant trying to understand how we can manipulate the
resonance frequency (see Figure 2.8.6). In section 2.5.2 of this chapter we found using

′
Drude-Lorentz’s model that the dielectric constant of low loss plasma (see (2.85)) is () ≈

2
2
1 − ⁄ . If so, the resonance frequency is = , i.e. it is defined by the number of free

electrons per volume unit. The
apparent way to develop such
metal-dielectric composite is to
immerse the lattice of electrically
small high conductive metal
(typically, Au, Ag, Al, Cu, or Pt)
particles of any shape (sphere,
Figure 2.8.7 Ring lattice, d – lattice period ellipsoid, disk, strip, rod, spiral,
ring, etc.) in host medium with