Page 118 - Maxwell House

98 Chapter 2

The next step is to introduce, at last formally, the graphene complex dielectric constant ()

following the expression (2.80) and assuming that = / and d = 0.34 nm

′ ′′
() + ′′ ′
() ≅ 1 − = 1 − = (1 + ⁄ ) − (2.103)
⁄
0
0

0 0
Note that the imaginary part of conductivity contributes to the real part of graphene permittivity.
We can see that () is negative in the entire frequency range in the same manner as for copper
′

(compare Figure 2.9.3 and 2.5.2). The absolute values of both () and () decrease with
′
′′

the increasing frequency in the transition from good conductor to semiconductor. We can expect
that graphene will become some kind of dielectric at higher frequencies. Indeed, its relative
permittivity in visible range is ≅ 5.5 − ( )⁄ 0 that gives ≅ 5.5 + 5.84 for the

wavelength of 546 nm. Note some essential graphene features without further elaboration:
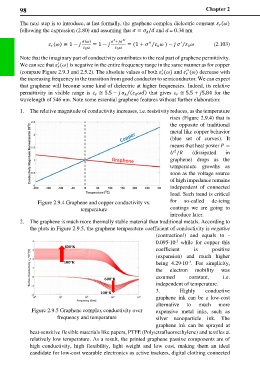
1. The relative magnitude of conductivity increases, i.e. resistivity reduces, as the temperature
rises (Figure 2.9.4) that is
the opposite of traditional
metal like copper behavior
(blue set of curves). It
means that heat power =
/ (dissipated in
2
graphene) drops as the
temperature growths as
soon as the voltage source
of high impedance remains
independent of connected
load. Such trend is critical
Figure 2.9.4 Graphene and copper conductivity vs. for so-called de-icing
temperature coatings we are going to
introduce later.
2. The graphene is much more thermally stable material than traditional metals. According to
the plots in Figure 2.9.5, the graphene temperature coefficient of conductivity is negative
(contraction!) and equals to -
-3
0.095∙10 while for copper this
60
coefficient is positive
(expansion) and much higher
1 being 4.29∙10 . For simplicity,
-3
the electron mobility was
assumed constant, i.e.
independent of temperature.
3. Highly conductive
graphene ink can be a low-cost
alternative to much more
Figure 2.9.5 Graphene complex conductivity over expensive metal inks, such as
frequency and temperature silver nanoparticle ink. The
graphene ink can be sprayed at
heat-sensitive flexible materials like papers, PTFE (Polytetrafluoroethylene) and textiles at
relatively low temperature. As a result, the printed graphene passive components are of
high conductivity, high flexibility, light weight and low cost, making them an ideal
candidate for low-cost wearable electronics as active trackers, digital clothing connected