Page 51 - Maxwell House

BASIC EQUATIONS OF MACROSCOPIC ELECTRODYNAMICS 31

∘ = (1.49)
0
Now, we can populate 3 Maxwell’s equations as well the new
rd
residents , and into the basement of Maxwell’s
0
q House, as shown in Figure 1.6.11a. Use the fact that the charge
qv - conservation law must be fair for any charges we can get the
conservation law and continuity equation for magnetic charges
using (1.8) – (1.10) as

= ∯ ∘ = − (1.50)

0

∘ + = 0 (1.51)
Figure 1.6.11b
Maxwell’s House The relationship (1.51) is incorporated in Maxwell’s House
basement, as shown in Figure 1.6.11b.
1.6.14 Magnetic Lines of Force
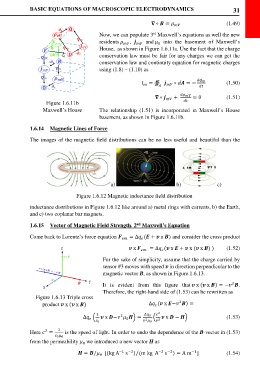
The images of the magnetic field distributions can be no less useful and beautiful than the

a) b) c)
Figure 1.6.12 Magnetic inductance field distribution

inductance distributions in Figure 1.6.12 like around a) metal rings with currents, b) the Earth,
and c) two coplanar bar magnets.

1.6.15 Vector of Magnetic Field Strength. 2 Maxwell’s Equation
nd
Come back to Lorentz’s force equation = Δ ( + x ) and consider the cross product

x = Δ ( x + x ( x ) ) (1.52)

For the sake of simplicity, assume that the charge carried by
sensor #3 moves with speed in direction perpendicular to the
magnetic vector B, as shown in Figure 1.6.13.
It is evident from this figure that x ( x ) = − .
2
Therefore, the right-hand side of (1.53) can be rewritten as
Figure 1.6.13 Triple cross
product x ( x ) Δ ( x − ) =
2

1 2 Δ 2
Δ � x − � = � x − � (1.53)

0
2
0 0 2
2 1 is the speed of light. In order to undo the dependence of the B-vector in (1.53)
Here =
0 0
from the permeability we introduced a new vector H as
0
= [(kg A s ) (m kg A s ) = A m ] (1.54)
−1
−1
−2
−2
−2
⁄
⁄
0