Page 133 - Mechatronics with Experiments

CLOSED LOOP CONTROL 119
r (s) y (s)
K e –t s 1/(s+1)
d
–

t d = 0.5;
Im (s)
e –tds 1
As K: 0 to infinity t d s+1
Im (s) 1 1
1+K = 0
t d = 0; t d s+1 s+1
1
1+K =0
s+1

Re (s) Re (s)
-1 –2 –1

(a) (b)

Im (s)
1+ K e -td s 1 =0
s+1
. .
t d = 0.5; . .
e –tds 1 2 Im (s) j3π t d
s+1)
(t d j2π t d
1 1
1+K 2 s+1 = 0
(t d s+1) jπ t d
Re (s) Re (s)
–2 –1 –1
–jπ t d

–j2π t d
–j3π t d
.
.
(c) . (d)
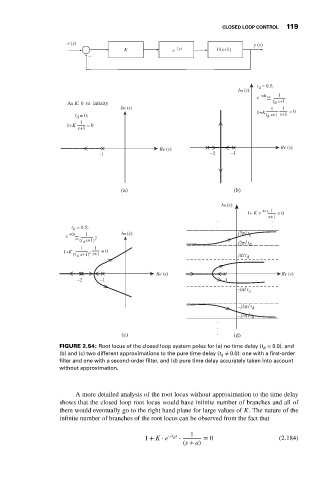
FIGURE 2.54: Root locus of the closed loop system poles for (a) no time delay (t = 0.0), and
d
(b) and (c) two different approximations to the pure time delay (t d ≠ 0.0): one with a first-order
filter and one with a second-order filter, and (d) pure time delay accurately taken into account
without approximation.

A more detailed analysis of the root locus without approximation to the time delay
shows that the closed loop root locus would have infinite number of branches and all of
them would eventually go to the right hand plane for large values of K. The nature of the
infinite number of branches of the root locus can be observed from the fact that
1
−t d s
1 + K ⋅ e ⋅ = 0 (2.184)
(s + a)