Page 135 - Mechatronics with Experiments

CLOSED LOOP CONTROL 121
Bode plot of pure time delay: exp(−1.0 s)
40
20
Mag (dB) 0

−20

−40
0
−90
Phase (deg) −180
−270
−360
−1 0 1
10 10 10
Frequency (rad/s)

exp(−1.0 s), 1/(s+1), exp(−1.0 s)/(s+1)
40

Mag (dB) 20 0

−20
0
−90
Phase (deg) −180

−270
−360
−1 0 1
10 10 10
Frequency (rad/s)
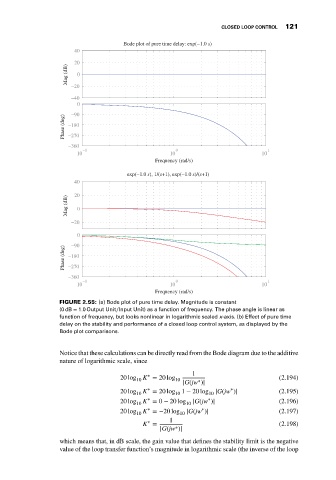
FIGURE 2.55: (a) Bode plot of pure time delay. Magnitude is constant
(0 dB = 1.0 Output Unit∕Input Unit) as a function of frequency. The phase angle is linear as
function of frequency, but looks nonlinear in logarithmic scaled x-axis. (b) Effect of pure time
delay on the stability and performance of a closed loop control system, as displayed by the
Bode plot comparisons.

Notice that these calculations can be directly read from the Bode diagram due to the additive
nature of logarithmic scale, since

∗
20 log K = 20 log 1 (2.194)
10 10 ∗
|G(jw )|
∗ ∗
10
20 log K = 20 log 1 − 20 log |G(jw )| (2.195)
10
10
∗ ∗
10
20 log K = 0 − 20 log |G(jw )| (2.196)
10
∗ ∗
10
20 log K =−20 log |G(jw )| (2.197)
10
1
∗
K = (2.198)
∗
|G(jw )|
which means that, in dB scale, the gain value that defines the stability limit is the negative
value of the loop transfer function’s magnitude in logarithmic scale (the inverse of the loop