Page 136 - Mechatronics with Experiments

122 MECHATRONICS
transfer function gain in linear scale) at the frequency where the loop transfer function has
◦
a phase angle of −180 .
Time delay is a serious problem in closed loop control systems in that it can make
an otherwise stable system unstable. In order to keep the system stable, loop gain must be
limited. Therefore, the overall price paid (to keep the system stable despite the time delay)
is lower bandwidth due to lower loop gain. If the time delay is known in advance accurately,
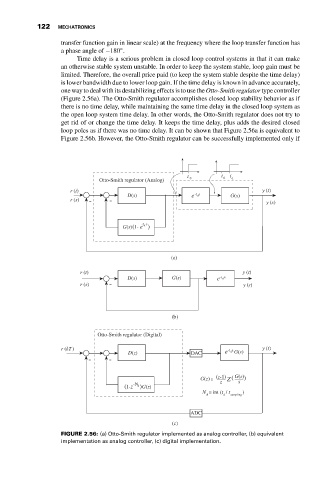
one way to deal with its destabilizing effects is to use the Otto-Smith regulator type controller
(Figure 2.56a). The Otto-Smith regulator accomplishes closed loop stability behavior as if
there is no time delay, while maintaining the same time delay in the closed loop system as
the open loop system time delay. In other words, the Otto-Smith regulator does not try to
get rid of or change the time delay. It keeps the time delay, plus adds the desired closed
loop poles as if there was no time delay. It can be shown that Figure 2.56a is equivalent to
Figure 2.56b. However, the Otto-Smith regulator can be successfully implemented only if

0 t t t
Otto-Smith regulator (Analog) 0 d
r (t) y (t)
D(s) e -t d s G(s)
r (s) - - y (s)

-t d s
G(s) (1- e )

(a)

r (t) y (t)
D(s) G(s) e -t d s
r (s) - y (s)

(b)

Otto-Smith regulator (Digital)
r (kT) -t y (t)
D(z) DAC e d s G(s)
- -

(z-1) ( G(s) )
Z
G(z)
=
z s
(1-z -N d ) G(z)
N = int (t / t )
d d sampling
ADC
(c)
FIGURE 2.56: (a) Otto-Smith regulator implemented as analog controller, (b) equivalent
implementation as analog controller, (c) digital implementation.