Page 128 - Mechatronics with Experiments

114 MECHATRONICS
series should be implemented. In other words, the derivative control may be modified as
u (s) = K se(s) (2.165)
d D
de(t)
u (t) = K ⋅ (2.166)
d
D
dt
which should be modified to reduce its high frequency gain, and hence reduce the noise
amplification of it,
1
u (s) = K s e(s) (2.167)
D
d
(K ∕N)s + 1
D
du (t) de(t)
(K ∕N) ⋅ d =−u (t) + K ⋅ (2.168)
D d D
dt dt
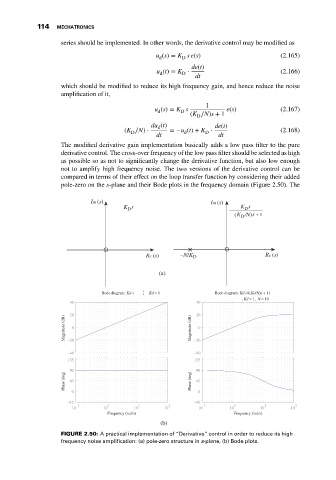
The modified derivative gain implementation basically adds a low pass filter to the pure
derivative control. The cross-over frequency of the low pass filter should be selected as high
as possible so as not to significantly change the derivative function, but also low enough
not to amplify high frequency noise. The two versions of the derivative control can be
compared in terms of their effect on the loop transfer function by considering their added
pole-zero on the s-plane and their Bode plots in the frequency domain (Figure 2.50). The

Im (s) Im (s)
K s K s
D D
( K /N) s + 1
D

Re (s) –N/K D Re (s)

(a)

Bode diagram: Kd s ; Kd = 1 Bode diagram: Kd s/((Kd/N)s + 1)
; Kd = 1, N = 10
40 40
20 20
Magnitude (dB) –20 0 Magnitude (dB) –20 0

–40 –40
135 135
90 90
Phase (deg) 45 Phase (deg) 45

0 0
–45 –45
–1 0 1 2 –1 0 1 2
10 10 10 10 10 10 10 10
Frequency (rad/s) Frequency (rad/s)
(b)
FIGURE 2.50: A practical implementation of “Derivative” control in order to reduce its high
frequency noise amplification: (a) pole-zero structure in s-plane, (b) Bode plots.