Page 785 - Mechatronics with Experiments

LABORATORY EXPERIMENTS 771
R = 220 Ω , 2.0 MΩ
4
R = 330 kΩ C = 0.22 μF
3
+9 V
– 1 kΩ
+
4.7 kΩ –9 V

100 kΩ 100 kΩ
V i
+9 V
1 kΩ 1 kΩ
–
1 kΩ
100 kΩ +
+9 V
–9 V 1 kΩ +9 V
V ref –
100 kΩ + – + V
–9 V o
1 kΩ –9 V
1 kΩ

C = 0.22 μF R = 4.7 kΩ
2
+9 V
R = 4.7 kΩ
1
–
+ 1 kΩ
–9 V
4.7 kΩ

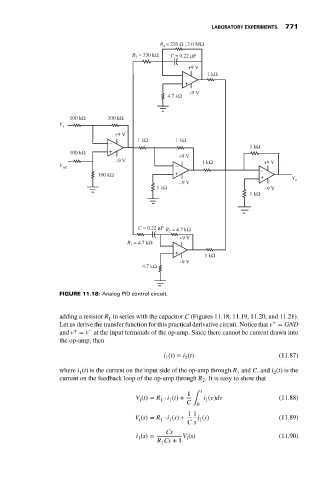
FIGURE 11.18: Analog PID control circuit.

adding a resistor R in series with the capacitor C (Figures 11.18, 11.19, 11.20, and 11.21).
1
+
Let us derive the transfer function for this practical derivative circuit. Notice that v = GND
+
−
and v = v at the input terminals of the op-amp. Since there cannot be current drawn into
the op-amp, then
i (t) = i (t) (11.87)
2
1
where i (t) is the current on the input side of the op-amp through R and C, and i (t)isthe
2
1
1
current on the feedback loop of the op-amp through R . It is easy to show that
2
t
1
V (t) = R ⋅ i (t) + C ∫ i ( )d (11.88)
1
1
1
i
0
1 1
V (s) = R ⋅ i (s) + i (s) (11.89)
i 1 1 1
C s
Cs
i (s) = V (s) (11.90)
i
1
R Cs + 1
1