Page 15 - Yusril Amron Flipbook Turunan Fungsi Aljabar dengan Pendekatan Kontekstual

Flipbook
Turunan Fungsi Aljabar dengan Pedekatan Kontekstual YUSRIL AMRON

C. Kemonotonan Fungsi

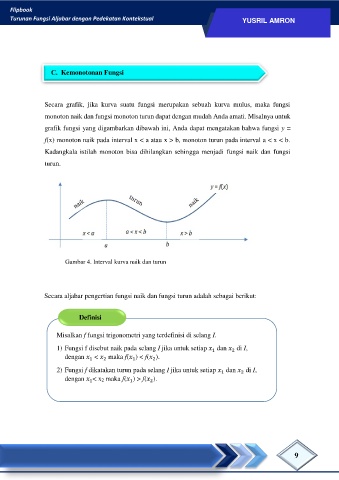
Secara grafik, jika kurva suatu fungsi merupakan sebuah kurva mulus, maka fungsi

monoton naik dan fungsi monoton turun dapat dengan mudah Anda amati. Misalnya untuk
grafik fungsi yang digambarkan dibawah ini, Anda dapat mengatakan bahwa fungsi y =

f(x) monoton naik pada interval x < a atau x > b, monoton turun pada interval a < x < b.
Kadangkala istilah monoton bisa dihilangkan sehingga menjadi fungsi naik dan fungsi

turun.

Gambar 4. Interval kurva naik dan turun

Secara aljabar pengertian fungsi naik dan fungsi turun adalah sebagai berikut:

Definisi

Misalkan f fungsi trigonometri yang terdefinisi di selang I.

1) Fungsi f disebut naik pada selang I jika untuk setiap dan di I,
1
2
dengan < maka f( ) < f( ).
2
2
1
1

2) Fungsi f dikatakan turun pada selang I jika untuk setiap dan di I,
1
2
dengan < x2 maka f( ) > f( ).
1
2
1

9