Page 60 - RTH3BA Preview

R���� T����� �������� - B������� �� A������� 3 �� E������.

One such algorithm is the "Taylor Series". It can be used to find sin(x).
Sin(x)= x-x3/3! + x5/5!-x7/7!..n

3! (3 factorial) Means 1 x 2 x 3, which is 6. 5! Means 1 x 2 x 3 x 4 x 5 = 120. I am
going to do this for one angle (30 degrees) and we are lucky there is a factorial key
on every scientific calculator {!}. See bottom page 598.

FINDING THE INSTANTANEOUS VALUES OF A SINE WAVE

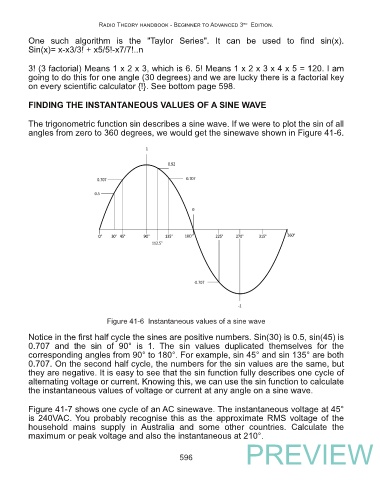
The trigonometric function sin describes a sine wave. If we were to plot the sin of all
angles from zero to 360 degrees, we would get the sinewave shown in Figure 41-6.

Figure 41-6 Instantaneous values of a sine wave

Notice in the first half cycle the sines are positive numbers. Sin(30) is 0.5, sin(45) is
0.707 and the sin of 90° is 1. The sin values duplicated themselves for the
corresponding angles from 90° to 180°. For example, sin 45° and sin 135° are both
0.707. On the second half cycle, the numbers for the sin values are the same, but
they are negative. It is easy to see that the sin function fully describes one cycle of
alternating voltage or current. Knowing this, we can use the sin function to calculate
the instantaneous values of voltage or current at any angle on a sine wave.

Figure 41-7 shows one cycle of an AC sinewave. The instantaneous voltage at 45°
is 240VAC. You probably recognise this as the approximate RMS voltage of the
household mains supply in Australia and some other countries. Calculate the
maximum or peak voltage and also the instantaneous at 210°.
PREVIEW

596