Page 32 - e-Book Analisis Real

Masalah 2

Diketahui fungsi f dengan

| |, ≠ 0
( ) = {
3 , = 0
Jelas fungsi f tak kontinu di x = 0, sebab lim f   x  f   0 .
x 0

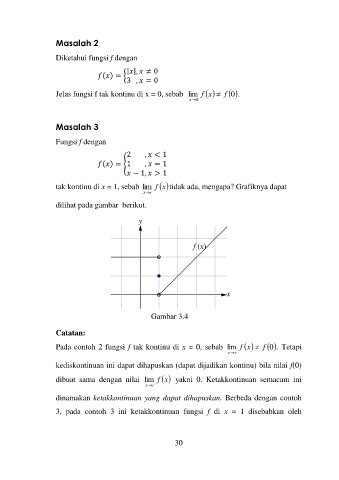
Masalah 3

Fungsi f dengan

2 , < 1
( ) = {1 , = 1
− 1, > 1

tak kontinu di x = 1, sebab lim f   x tidak ada, mengapa? Grafiknya dapat
x c
dilihat pada gambar berikut.

y

f (x)

x

Gambar 3.4

Catatan:

Pada contoh 2 fungsi f tak kontinu di x = 0, sebab lim f   x  f   0 . Tetapi
x c
kediskontinuan ini dapat dihapuskan (dapat dijadikan kontinu) bila nilai f(0)

dibuat sama dengan nilai lim f   x yakni 0. Ketakkontinuan semacam ini
x c

dinamakan ketakkontinuan yang dapat dihapuskan. Berbeda dengan contoh
3, pada contoh 3 ini ketakkontinuan fungsi f di x = 1 disebabkan oleh

30