Page 39 - Ekonomi SMA Kelas XI Rev

dari 12–17 persen maka distribusi pendapatan dikategorikan
sebagai ketimpangan pendapatan sedang/menengah.
3) Jika proporsi jumlah pendapatan dari penduduk yang masuk
kategori 40 persen terendah terhadap total pendapatan selu-
ruh penduduk kurang dari 17 persen dikategorikan sebagai
ketimpangan pendapatan rendah.
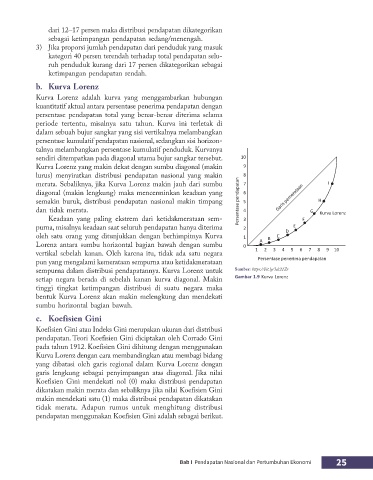
b. Kurva Lorenz
Kurva Lorenz adalah kurva yang menggambarkan hubungan
kuantitatif aktual antara persentase penerima pendapatan dengan
persentase pendapatan total yang benar-benar diterima selama
periode tertentu, misalnya satu tahun. Kurva ini terletak di
dalam sebuah bujur sangkar yang sisi vertikalnya melambangkan
persentase kumulatif pendapatan nasional, sedangkan sisi horizon-
talnya melambangkan persentase kumulatif penduduk. Kurvanya
sendiri ditempatkan pada diagonal utama bujur sangkar tersebut. 10
Kurva Lorenz yang makin dekat dengan sumbu diagonal (makin 9
lurus) menyiratkan distribusi pendapatan nasional yang makin 8
merata. Sebaliknya, jika Kurva Lorenz makin jauh dari sumbu 7 I
diagonal (makin lengkung) maka mencerminkan keadaan yang 6 Garis pemerataan
semakin buruk, distribusi pendapatan nasional makin timpang Persentase pendapatan 5 H
dan tidak merata. 4 G Kurva Lorenz
Keadaan yang paling ekstrem dari ketidakmerataan sem- 3 F
purna, misalnya keadaan saat seluruh pendapatan hanya diterima 2 D E
oleh satu orang yang ditunjukkan dengan berhimpitnya Kurva 1 B C
A
Lorenz antara sumbu horizontal bagian bawah dengan sumbu 0
1 2 3 4 5 6 7 8 9 10
vertikal sebelah kanan. Oleh karena itu, tidak ada satu negara
Persentase penerima pendapatan
pun yang mengalami kemerataan sempurna atau ketidakmerataan
sempurna dalam distribusi pendapatannya. Kurva Lorenz untuk Sumber: https://bit.ly/3dc21Zr
Gambar 1.9 Kurva Lorenz
setiap negara berada di sebelah kanan kurva diagonal. Makin
tinggi tingkat ketimpangan distribusi di suatu negara maka
bentuk Kurva Lorenz akan makin melengkung dan mendekati
sumbu horizontal bagian bawah.
c. Koefisien Gini

Koefisien Gini atau Indeks Gini merupakan ukuran dari distribusi
pendapatan. Teori Koefisien Gini diciptakan oleh Corrado Gini
pada tahun 1912. Koefisien Gini dihitung dengan menggunakan
Kurva Lorenz dengan cara membandingkan atau membagi bidang
yang dibatasi oleh garis regional dalam Kurva Lorenz dengan
garis lengkung sebagai penyimpangan atas diagonal. Jika nilai
Koefisien Gini mendekati nol (0) maka distribusi pendapatan
dikatakan makin merata dan sebaliknya jika nilai Koefisien Gini
makin mendekati satu (1) maka distribusi pendapatan dikatakan
tidak merata. Adapun rumus untuk menghitung distribusi
pendapatan menggunakan Koefisien Gini adalah sebagai berikut.

Bab I Pendapatan Nasional dan Pertumbuhan Ekonomi 25