Page 108 - RM 1° Sec GM

Capítulo 24

Perímetro de figuras

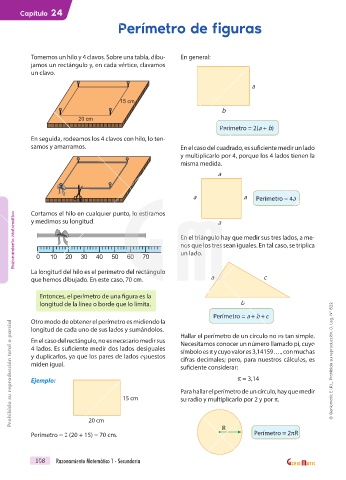
Tomemos un hilo y 4 clavos. Sobre una tabla, dibu- En general:
jamos un rectángulo y, en cada vértice, clavamos
un clavo.

a

15 cm
b
20 cm
Perímetro = 2(a + b)
En seguida, rodeamos los 4 clavos con hilo, lo ten-
samos y amarramos. En el caso del cuadrado, es suficiente medir un lado
y multiplicarlo por 4, porque los 4 lados tienen la
misma medida.
a

a a Perímetro = 4a

Cortamos el hilo en cualquier punto, lo estiramos
Razonamiento Matemático y medimos su longitud. En el triángulo hay que medir sus tres lados, a me-
a

nos que los tres sean iguales. En tal caso, se triplica
un lado.
40
30
70
60
50
10
0
20
La longitud del hilo es el perímetro del rectángulo
que hemos dibujado. En este caso, 70 cm. a c
Entonces, el perímetro de una figura es la
longitud de la línea o borde que lo limita. b
Perímetro = a + b + c
Otro modo de obtener el perímetro es midiendo la
Prohibida su reproducción total o parcia l
longitud de cada uno de sus lados y sumándolos.
Hallar el perímetro de un círculo no es tan simple.
En el caso del rectángulo, no es necesario medir sus Necesitamos conocer un número llamado pi, cuyo
4 lados. Es suficiente medir dos lados desiguales símbolo es  y cuyo valor es 3,14159…., con muchas
y duplicarlos, ya que los pares de lados opuestos cifras decimales; pero, para nuestros cálculos, es
miden igual. suficiente considerar:  Geniomatic E.I.R.L. Prohibida su reproducción. D. Leg. N° 822

Ejemplo:  = 3,14

Para hallar el perímetro de un círculo, hay que medir
15 cm su radio y multiplicarlo por 2 y por .

20 cm
R
Perímetro = 2 (20 + 15) = 70 cm. Perímetro = 2R

108 Razonamiento Matemático 1 - Secundaria