Page 136 - Matematica 1° Sec

Funciones III

En una función y = f(x), el rango es el conjunto de valores que toma y.

El rango de la función del ejemplo es Rf = {–3; –2; –1; 0; 1}.

Actividad 24

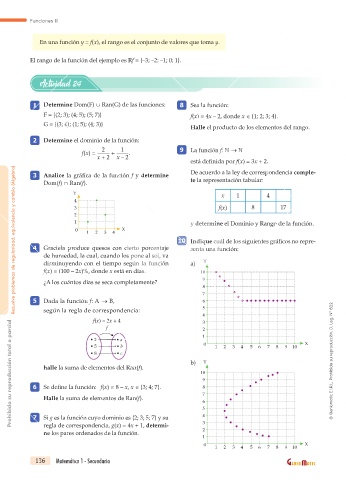
1 Determine Dom(F)  Ran(G) de las funciones: 8 Sea la función:
F = {(2; 3); (4; 5); (5; 7)} f(x) = 4x – 2, donde x ∈ {1; 2; 3; 4}.
G = {(3; 6); (1; 5); (4; 3)}
Halle el producto de los elementos del rango.

2 Determine el dominio de la función:
2 1
f(x) = + . 9 La función f:  → 
x + 2 x – 2
está definida por f(x) = 3x + 2.
Resuelve problemas de regularidad, equivalencia y cambio (Álgebra)
De acuerdo a la ley de correspondencia comple-
3 Analice la gráfica de la función f y determine
Dom(f)  Ran(f). te la representación tabular:
Y x 1 4
4
3 f(x) 8 17
2
1 y determine el Dominio y Rango de la función.
0 X
1 2 3 4
10 Indique cuál de los siguientes gráficos no repre-
4 Graciela produce quesos con cierto porcentaje senta una función:
de humedad, la cual, cuando los pone al sol, va
disminuyendo con el tiempo según la función a) Y
f(x) = (100 – 2x)%, donde x está en días. 10

¿A los cuántos días se seca completamente? 9
8
7
5 Dada la función f: A → B, 6
según la regla de correspondencia: 5
4
f(x) = 2x + 4 3
Prohibida su reproducción total o parcia l
f
2
1
• 2 • a
• 5 • b 0 1 2 3 4 5 6 7 8 9 10 X
• 8 • c

b) Y  Geniomatic E.I.R.L. Prohibida su reproducción. D. Leg. N° 822
halle la suma de elementos del Ran(f).
10
9
6 Se define la función: f(x) = 8 – x, x ∈ {3; 4; 7}. 8
7
Halle la suma de elementos de Ran(f).
6
5
7 Si g es la función cuyo dominio es {2; 3; 5; 7} y su 4
regla de correspondencia, g(x) = 4x + 1, determi- 3
ne los pares ordenados de la función. 2
1
0 X
1 2 3 4 5 6 7 8 9 10
136 Matemática 1 - Secundaria