Page 93 - KALKULUS 2 EMY SOHILAIT

Definisi
1. Andaikan f kontinu pada selang setengah buka [a, b) dan andaikan

(x )  
lim f
x b 
b t
Maka,
 f ( x) dx  lim   f ( x) dx
a t b a

Asalkan limit ini ada dan terhingga. Dalam hal ini dikatakan bahwa integral

tersebut konvergen. Dalam hal yang lain disebut divergen.

2. Andaikan f kontinu pada selang setengah buka (a, b] dan andaikan
lim f (x )   .

x a 
Maka, b b
 x)  lim   f ( x) dx
dx
f (
a t a t

Asalkan limit ini ada dan terhingga. Dalam hal ini dikatakan bahwa integral
tersebut konvergen. Dalam hal yang lain disebut divergen.

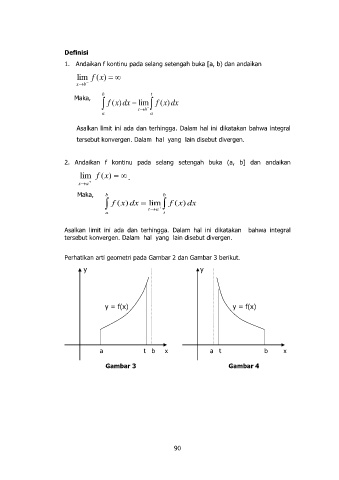
Perhatikan arti geometri pada Gambar 2 dan Gambar 3 berikut.
y y

y = f(x) y = f(x)

a t b x a t b x

Gambar 3 Gambar 4

90