Page 19 - June

METALWORKING EQUIPMENT AND TOOLS

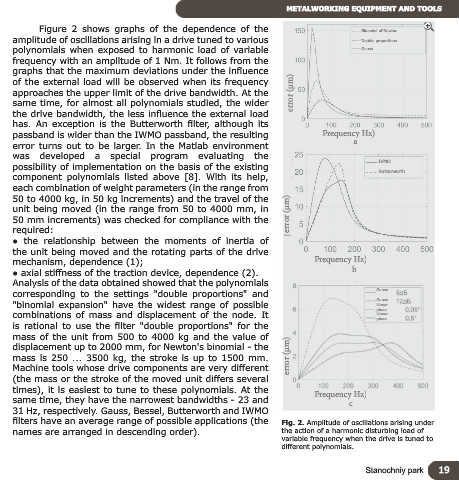
Figure 2 shows graphs of the dependence of the Binomial of Newton
amplitude of oscillations arising in a drive tuned to various Double proportions
polynomials when exposed to harmonic load of variable Gauss
frequency with an amplitude of 1 Nm. It follows from the
graphs that the maximum deviations under the influence
of the external load will be observed when its frequency
approaches the upper limit of the drive bandwidth. At the error (μm)
same time, for almost all polynomials studied, the wider
the drive bandwidth, the less influence the external load
has. An exception is the Butterworth filter, although its
passband is wider than the IWMO passband, the resulting Frequency Hz)
error turns out to be larger. In the Matlab environment a
was developed a special program evaluating the
possibility of implementation on the basis of the existing IVMO
component polynomials listed above [8]. With its help, Butterworth
each combination of weight parameters (in the range from
50 to 4000 kg, in 50 kg increments) and the travel of the
unit being moved (in the range from 50 to 4000 mm, in
50 mm increments) was checked for compliance with the error (μm)
required:
● the relationship between the moments of inertia of
the unit being moved and the rotating parts of the drive
mechanism, dependence (1); Frequency Hz)
● axial stiffness of the traction device, dependence (2). b
Analysis of the data obtained showed that the polynomials
corresponding to the settings "double proportions" and Gauss
"binomial expansion" have the widest range of possible Gauss
Linear
combinations of mass and displacement of the node. It phase
Linear
phase
is rational to use the filter "double proportions" for the
mass of the unit from 500 to 4000 kg and the value of
displacement up to 2000 mm, for Newton's binomial - the
mass is 250 ... 3500 kg, the stroke is up to 1500 mm. error (μm)
Machine tools whose drive components are very different
(the mass or the stroke of the moved unit differs several
times), it is easiest to tune to these polynomials. At the Frequency Hz)
same time, they have the narrowest bandwidths - 23 and c
31 Hz, respectively. Gauss, Bessel, Butterworth and IWMO
filters have an average range of possible applications (the Fig. 2. Amplitude of oscillations arising under
names are arranged in descending order). the action of a harmonic disturbing load of
variable frequency when the drive is tuned to
different polynomials.

Stanochniy park 19