Page 580 - Krugmans Economics for AP Text Book_Neat

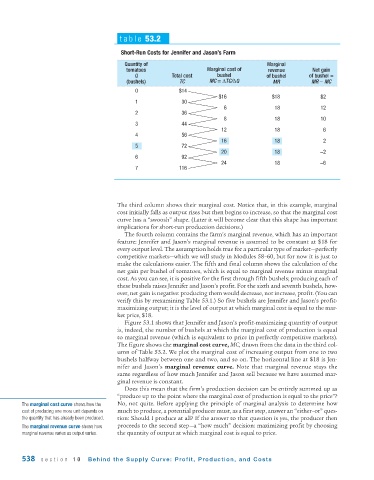
table 53.2

Short -Run Costs for Jennifer and Jason’s Farm

Quantity of Marginal
tomatoes Marginal cost of revenue Net gain
Q Total cost bushel of bushel of bushel =
(bushels) TC MC = ΔTC/ΔQ MR MR − MC
0 $14
$16 $18 $2
1 30
6 18 12
2 36
8 18 10
3 44
12 18 6
4 56
16 18 2
5 72
20 18 −2
6 92
24 18 −6
7 116

The third column shows their marginal cost. Notice that, in this example, marginal
cost initially falls as output rises but then begins to increase, so that the marginal cost
curve has a “swoosh” shape. (Later it will become clear that this shape has important
implications for short-run production decisions.)
The fourth column contains the farm’s marginal revenue, which has an important
feature: Jennifer and Jason’s marginal revenue is assumed to be constant at $18 for
every output level. The assumption holds true for a particular type of market—perfectly
competitive markets—which we will study in Modules 58–60, but for now it is just to
make the calculations easier. The fifth and final column shows the calculation of the
net gain per bushel of tomatoes, which is equal to marginal revenue minus marginal
cost. As you can see, it is positive for the first through fifth bushels; producing each of
these bushels raises Jennifer and Jason’s profit. For the sixth and seventh bushels, how-
ever, net gain is negative: producing them would decrease, not increase, profit. (You can
verify this by reexamining Table 53.1.) So five bushels are Jennifer and Jason’s profit-
maximizing output; it is the level of output at which marginal cost is equal to the mar-
ket price, $18.
Figure 53.1 shows that Jennifer and Jason’s profit-maximizing quantity of output
is, indeed, the number of bushels at which the marginal cost of production is equal
to marginal revenue (which is equivalent to price in perfectly competitive markets).
The figure shows the marginal cost curve, MC, drawn from the data in the third col-
umn of Table 53.2. We plot the marginal cost of increasing output from one to two
bushels halfway between one and two, and so on. The horizontal line at $18 is Jen-
nifer and Jason’s marginal revenue curve. Note that marginal revenue stays the
same regardless of how much Jennifer and Jason sell because we have assumed mar-
ginal revenue is constant.
Does this mean that the firm’s production decision can be entirely summed up as
“produce up to the point where the marginal cost of production is equal to the price”?
The marginal cost curve shows how the No, not quite. Before applying the principle of marginal analysis to determine how
cost of producing one more unit depends on much to produce, a potential producer must, as a first step, answer an “either–or” ques-
the quantity that has already been produced. tion: Should I produce at all? If the answer to that question is yes, the producer then
The marginal revenue curve shows how proceeds to the second step—a “how much” decision: maximizing profit by choosing
marginal revenue varies as output varies. the quantity of output at which marginal cost is equal to price.

538 section 10 Behind the Supply Curve: Profit, Production, and Costs