Page 579 - Krugmans Economics for AP Text Book_Neat

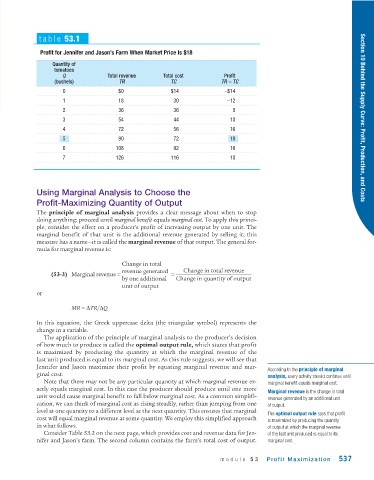
table 53.1

Profit for Jennifer and Jason’s Farm When Market Price Is $18

Quantity of
tomatoes
Q Total revenue Total cost Profit
(bushels) TR TC TR − TC
0 $0 $14 −$14
1 18 30 −12
2 36 36 0
3 54 44 10 Section 10 Behind the Supply Curve: Profit, Production, and Costs
4 72 56 16
5 90 72 18
6 108 92 16
7 126 116 10

Using Marginal Analysis to Choose the
Profit-Maximizing Quantity of Output
The principle of marginal analysis provides a clear message about when to stop
doing anything: proceed until marginal benefit equals marginal cost. To apply this princi-
ple, consider the effect on a producer’s profit of increasing output by one unit. The
marginal benefit of that unit is the additional revenue generated by selling it; this
measure has a name—it is called the marginal revenue of that output. The general for-
mula for marginal revenue is:

Change in total
(53-3) Marginal revenue = revenue generated = Change in total revenue
by one additional Change in quantity of output
unit of output
or

MR =ΔTR/ΔQ

In this equation, the Greek uppercase delta (the triangular symbol) represents the
change in a variable.
The application of the principle of marginal analysis to the producer’s decision
of how much to produce is called the optimal output rule, which states that profit
is maximized by producing the quantity at which the marginal revenue of the
last unit produced is equal to its marginal cost. As this rule suggests, we will see that
Jennifer and Jason maximize their profit by equating marginal revenue and mar-
According to the principle of marginal
ginal cost. analysis, every activity should continue until
Note that there may not be any particular quantity at which marginal revenue ex- marginal benefit equals marginal cost.
actly equals marginal cost. In this case the producer should produce until one more
Marginal revenue is the change in total
unit would cause marginal benefit to fall below marginal cost. As a common simplifi- revenue generated by an additional unit
cation, we can think of marginal cost as rising steadily, rather than jumping from one of output.
level at one quantity to a different level at the next quantity. This ensures that marginal
The optimal output rule says that profit
cost will equal marginal revenue at some quantity. We employ this simplified approach is maximized by producing the quantity
in what follows. of output at which the marginal revenue
Consider Table 53.2 on the next page, which provides cost and revenue data for Jen- of the last unit produced is equal to its
nifer and Jason’s farm. The second column contains the farm’s total cost of output. marginal cost.

module 53 Profit Maximization 537