Page 80 - Krugmans Economics for AP Text Book_Neat

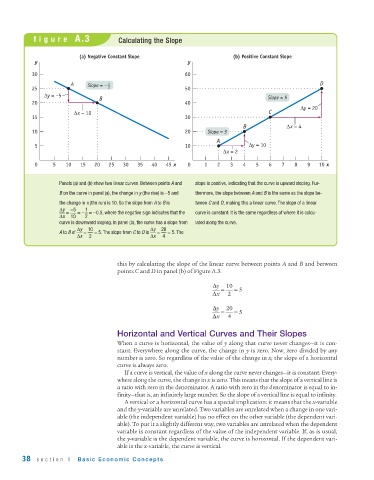
figure A.3 Calculating the Slope

(a) Negative Constant Slope (b) Positive Constant Slope
y y
30 60

A Slope = – 1 D
25 2 50
Δy = –5 Slope = 5
20 B 40
Δy = 20
Δx = 10 C
15 30
B Δx = 4
10 20 Slope = 5
A
5 10 Δy = 10
Δx = 2

0 5 10 15 20 25 30 35 40 45 x 0 1 2 3 4 5 6 7 8 9 10 x

Panels (a) and (b) show two linear curves. Between points A and slope is positive, indicating that the curve is upward sloping. Fur-
B on the curve in panel (a), the change in y (the rise) is −5 and thermore, the slope between A and B is the same as the slope be-
the change in x (the run) is 10. So the slope from A to B is tween C and D, making this a linear curve. The slope of a linear
Δy −5 1
= = − = −0.5, where the negative sign indicates that the curve is constant: it is the same regardless of where it is calcu-
Δx 10 2
curve is downward sloping. In panel (b), the curve has a slope from lated along the curve.
Δy 10 Δy 20
A to B of = = 5. The slope from C to D is = = 5. The
Δx 2 Δx 4

this by calculating the slope of the linear curve between points A and B and between
points C and D in panel (b) of Figure A.3.

Δy = 10 = 5
Δx 2
Δy = 20 = 5
Δx 4

Horizontal and Vertical Curves and Their Slopes

When a curve is horizontal, the value of y along that curve never changes—it is con-
stant. Everywhere along the curve, the change in y is zero. Now, zero divided by any
number is zero. So regardless of the value of the change in x, the slope of a horizontal
curve is always zero.
If a curve is vertical, the value of x along the curve never changes—it is constant. Every-
where along the curve, the change in x is zero. This means that the slope of a vertical line is
a ratio with zero in the denominator. A ratio with zero in the denominator is equal to in-
finity—that is, an infinitely large number. So the slope of a vertical line is equal to infinity.
A vertical or a horizontal curve has a special implication: it means that the x-variable
and the y-variable are unrelated. Two variables are unrelated when a change in one vari-
able (the independent variable) has no effect on the other variable (the dependent vari-
able). To put it a slightly different way, two variables are unrelated when the dependent
variable is constant regardless of the value of the independent variable. If, as is usual,
the y-variable is the dependent variable, the curve is horizontal. If the dependent vari-
able is the x-variable, the curve is vertical.
38 section I Basic Economic Concepts