Page 82 - Krugmans Economics for AP Text Book_Neat

which gets flatter. A curve that is upward sloping and gets steeper, as in panel (a), is
said to have positive increasing slope. A curve that is upward sloping but gets flatter, as in
panel (b), is said to have positive decreasing slope.
When we calculate the slope along these nonlinear curves, we obtain different values
for the slope at different points. How the slope changes along the curve determines the
curve’s shape. For example, in panel (a) of Figure A.4, the slope of the curve is a positive
number that steadily increases as the line moves from left to right, whereas in panel (b),
the slope is a positive number that steadily decreases.
The slopes of the curves in panels (c) and (d) are negative numbers. Economists
often prefer to express a negative number as its absolute value, which is the value of
the negative number without the minus sign. In general, we denote the absolute value
of a number by two parallel bars around the number; for example, the absolute value of
−4 is written as |−4| = 4. In panel (c), the absolute value of the slope steadily increases
as the line moves from left to right. The curve therefore has negative increasing slope.
And in panel (d), the absolute value of the slope of the curve steadily decreases along
the curve. This curve therefore has negative decreasing slope.

Maximum and Minimum Points

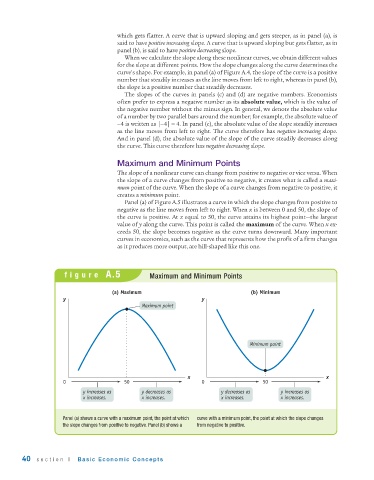
The slope of a nonlinear curve can change from positive to negative or vice versa. When
the slope of a curve changes from positive to negative, it creates what is called a maxi-
mum point of the curve. When the slope of a curve changes from negative to positive, it
creates a minimum point.
Panel (a) of Figure A.5 illustrates a curve in which the slope changes from positive to
negative as the line moves from left to right. When x is between 0 and 50, the slope of
the curve is positive. At x equal to 50, the curve attains its highest point—the largest
value of y along the curve. This point is called the maximum of the curve. When x ex-
ceeds 50, the slope becomes negative as the curve turns downward. Many important
curves in economics, such as the curve that represents how the profit of a firm changes
as it produces more output, are hill-shaped like this one.

figure A.5 Maximum and Minimum Points

(a) Maximum (b) Minimum
y y
Maximum point

Minimum point

x x
0 50 0 50

y increases as y decreases as y decreases as y increases as
x increases. x increases. x increases. x increases.

Panel (a) shows a curve with a maximum point, the point at which curve with a minimum point, the point at which the slope changes
the slope changes from positive to negative. Panel (b) shows a from negative to positive.

40 section I Basic Economic Concepts