Page 7 - complejos

unidad 6
números complejos
3. Representación gráfica
3. Representación gráfica

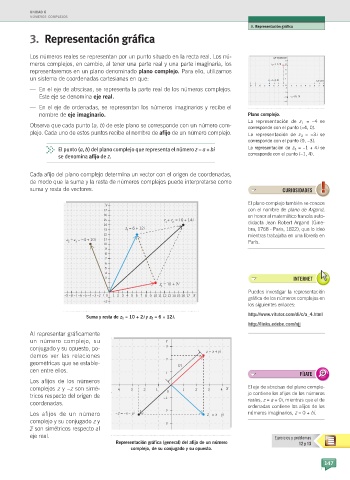
Los números reales se representan por un punto situado en la recta real. Los nú­ Eje imaginario
5
meros complejos, en cambio, al tener una parte real y una parte imaginaria, los z 3 = (–1, 4) 4
representaremos en un plano denominado plano complejo. Para ello, utilizamos 3
2
un sistema de coordenadas cartesianas en que: z 1 = (–4, 0) 1 Eje real
–8 –7 –6 –5 –4 –3 –2 –1 0 1 2 3 4 5 6 7 8
— En el eje de abscisas, se representa la parte real de los números complejos. –1
–2
Este eje se denomina eje real. –3 z 2 = (0,–3)
–4
— En el eje de ordenadas, se representan los números imaginarios y recibe el
nombre de eje imaginario. Plano complejo.
La representación de z 1 = -4 se
Observa que cada punto (a, b) de este plano se corresponde con un número com­ corresponde con el punto (-4, 0).
plejo. Cada uno de estos puntos recibe el nombre de afijo de un número complejo. La representación de z 2 = -3i se
corresponde con el punto (0, -3).
q q El punto (a, b) del plano complejo que representa el número z = a + bi La representación de z 3 = -1 + 4i se
se denomina afijo de z. corresponde con el punto (-1, 4).

Cada afijo del plano complejo determina un vector con el origen de coordenadas,
de modo que la suma y la resta de números complejos puede interpretarse como
suma y resta de vectores. CURIOSIDADES

El plano complejo también se conoce
Y
17 con el nombre de plano de Argand,
16 en honor al matemático francés auto­
15 z + z = 16 + 14i didacta Jean Robert Argand (Gine­
2
1
14
13 z = 6 + 12i bra, 1768 ­ París, 1822), que lo ideó
2
12 mientras trabajaba en una librería en
z – z = –4 + 10i 11 París.
2
1
10
9
8
7
6
5
4
3 INTERNET
z = 10 + 2i
1
Puedes investigar la representación
–9 –8 –7 –6 –5 –4 –3 –2 –1 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 X gráfica de los números complejos en
–2
los siguientes enlaces:
http://www.vitutor.com/di/c/a_4.html
Suma y resta de z 1 = 10 + 2i y z 2 = 6 + 12i.
http://links.edebe.com/njj
Al representar gráficamente
un número complejo, su Y
conjugado y su opuesto, po­ 3 z = x + yi
demos ver las relaciones
geométricas que se estable­ 2 |z|
cen entre ellos.
1 FÍJATE
Los afijos de los números
complejos z y -z son simé­ –4 –3 –2 –1 0 1 2 3 4 X El eje de abscisas del plano comple­
tricos respecto del origen de –1 jo contiene los afijos de los números
coordenadas. reales, z = a + 0i, mientras que el de
ordenadas contiene los afijos de los
–2
Los afijos de un número –z = –x – yi z – = x – yi números imaginarios, z = 0 + bi.
complejo y su conjugado z y –3
z son simétricos respecto al
eje real. Ejercicios y problemas
Representación gráfica (general) del afijo de un número 12 y 13
complejo, de su conjugado y su opuesto.

147