Page 8 - complejos

bloque 2
geometría

FÍJATE 5 EJEMPLO
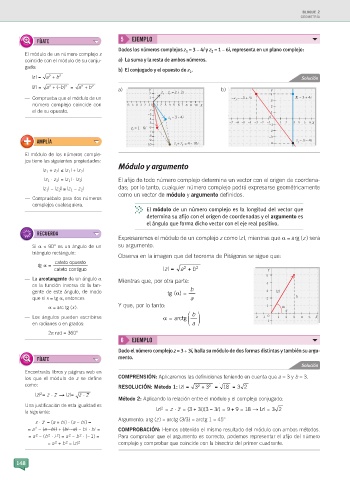
Dados los números complejos z 1 = 3 - 4i y z 2 = 1 - 6i, representa en un plano complejo:
El módulo de un número complejo z
coincide con el módulo de su conju­ a) La suma y la resta de ambos números.
gado:
b) El conjugado y el opuesto de z 1 .
2
|z| = a + b 2 Solución
2
2
|z | = a + (−b) 2 = a + b 2 a) Y b) Y
2 z 1 – z 2 = 2 + 2i 4
— Comprueba que el módulo de un 1 –z 1 = –3 + 4i 3 z 1 = 3 + 4i
número complejo coincide con –6 –5 –4 –3 –2 –1 0 1 2 3 4 5 6 7 8 9 10 X 2
el de su opuesto. –2 1
–3
–4 z 1 = 3 – 4i 0
–5 –7 –6 –5 –4 –3 –2 –1 –1 1 2 3 4 5 6 X
z 2 = 1 – 6i –6
–7 –2
–8 –3
AMPLÍA –9 z 1 = 3 – 4i
AMPLÍA
–10 z 1 + z 2 = 4 – 10i –4
El módulo de los números comple­
jos tiene las siguientes propiedades:
Módulo y argumento
|z 1 + z 2 | ≤ |z 1 | + |z 2 |
|z 1 · z 2 | = |z 1 | · |z 2 | El afijo de todo número complejo determina un vector con el origen de coordena­
|z 1 | - |z 2 | ≤ |z 1 - z 2 | das; por lo tanto, cualquier número complejo podrá expresarse geométricamente
como un vector de módulo y argumento definidos.
— Compruébalo para dos números
complejos cualesquiera.
q q El módulo de un número complejo es la longitud del vector que
determina su afijo con el origen de coordenadas y el argumento es
el ángulo que forma dicho vector con el eje real positivo.
RECUERDA
Expresaremos el módulo de un complejo z como |z |, mientras que a = arg (z ) será
— Si a < 90° es un ángulo de un su argumento.
triángulo rectángulo:
Observa en la imagen que del teorema de Pitágoras se sigue que:
cateto opuesto
tg α =
2
cateto contiguo |z| = a + b 2 Y
5
— La arcotangente de un ángulo a Mientras que, por otra parte:
es la función inversa de la tan­ 4
gente de este ángulo, de modo tg (α) = b 3 |z|
que si x = tg a, entonces a 2 b
a = arc tg (x ). Y que, por lo tanto: 1 α a
⎛ b ⎞
— Los ángulos pueden escribirse α = arctg ⎜ ⎟ –2 –1 0 1 2 3 4 5 X
en radianes o en grados: ⎝ a ⎠ –1
2p rad = 360°
6 EJEMPLO

Dado el número complejo z = 3 + 3i, halla su módulo de dos formas distintas y también su argu-
FÍJATE mento.
Solución
Encontrarás libros y páginas web en
los que el módulo de z se define COMPRENSIÓN: Aplicaremos las definiciones teniendo en cuenta que a = 3 y b = 3.
como: RESOLUCIÓN: Método 1: |z| = 3 + 3 2 = 18 = 3 2
2
2
|z| = z · z S |z|= z · z
Método 2: Aplicando la relación entre el módulo y el complejo conjugado:
Una justificación de esta igualdad es 2
la siguiente: |z| = z · z = (3 + 3i)(3 − 3i) = 9 + 9 = 18 S |z| = 3 2
Argumento: arg (z ) = arctg (3/3) = arctg 1 = 45°
z · z = (a + bi ) · (a - bi ) =
= a - (a · bi ) + (bi · a) - bi · bi = COMPROBACIÓN: Hemos obtenido el mismo resultado del módulo con ambos métodos.
2
2
2
2
2
= a - (b · i ) = a - b · (- 1) = Para comprobar que el argumento es correcto, podemos representar el afijo del número
2
2
= a + b = |z | 2 complejo y comprobar que coincide con la bisectriz del primer cuadrante.
2
148