Page 111 - E-Modul Kalkulus Integral
P. 111
e-Modul Kalkulus Integral
Program Studi Pendidikan Matematika
Daerah yang terbentuk dari kurva =
2
2
=
dan = 1 − ( − 1) terlihat seperti pada
2
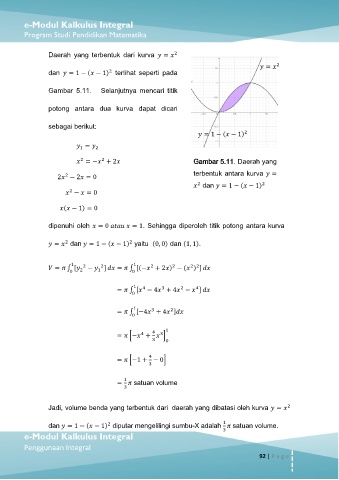
Gambar 5.11. Selanjutnya mencari titik
potong antara dua kurva dapat dicari
sebagai berikut:
2
= 1 − ( − 1)
=
2
1
= − + 2 Gambar 5.11. Daerah yang
2
2
2 − 2 = 0 terbentuk antara kurva =
2
dan = 1 − ( − 1)
2
2
− = 0
2
( − 1) = 0
dipenuhi oleh = 0 = 1. Sehingga diperoleh titik potong antara kurva
= dan = 1 − ( − 1) yaitu (0, 0) dan (1, 1).
2
2
1 1
2
2
2 2
2
= ∫ [ 2 − ] = ∫ [(− + 2 ) − ( ) ]
0 2 1 0
1
= ∫ [ − 4 + 4 − ]
2
4
3
4
0
1
= ∫ [−4 + 4 ]
3
2
0
1
4
= [− + ]
4
3
3 0
4
= [−1 + − 0]
3
1
= satuan volume
3
Jadi, volume benda yang terbentuk dari daerah yang dibatasi oleh kurva =
2
1
dan = 1 − ( − 1) diputar mengelilingi sumbu-X adalah satuan volume.
2
3
e-Modul Kalkulus Integral
Penggunaan Integral
92 | P a g e