Page 21 - E-Modul Kalkulus Integral

e-Modul Kalkulus Integral
Program Studi Pendidikan Matematika

1.1 Anti Turunan/ Integral Tak Tentu
Untuk memahami integral tak tentu sebagai anti turunan, perhatikan tabel

dan gambar pada kasus berikut ini. Diketahui fungsi dan turunannya:

Fungsi Turunan

( ) = + 1 2
2
2
( ) = 2
2
( ) = − 1 2
2
( ) = + 2

dari tabel di atas terlihat bahwa fungsi ( ), ( ), ( ) dengan nilai yang

berbeda memiliki turunan yang sama.

2
( ) = + 1

2
( ) =

2
( ) = − 1

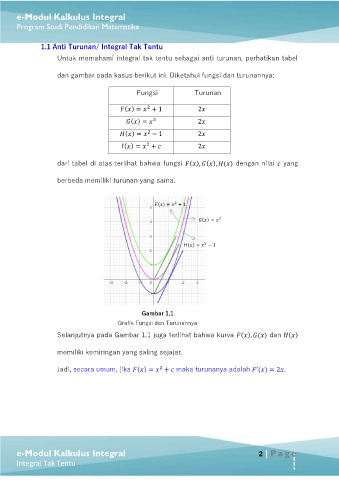
Gambar 1.1

Grafik Fungsi dan Turunannya

Selanjutnya pada Gambar 1.1 juga terlihat bahwa kurva ( ), ( ) dan ( )

memiliki kemiringan yang saling sejajar.

2
Jadi, secara umum, jika ( ) = + maka turunanya adalah ′( ) = 2 .

e-Modul Kalkulus Integral 2 | P a g e

Integral Tak Tentu