Page 22 - E-Modul Kalkulus Integral

e-Modul Kalkulus Integral
Program Studi Pendidikan Matematika

Sifat 1: Misalkan ( ) dan ( ) dua buah fungsi dengan sifat ′( ) = ′( ) maka
terdapat konstanta sehingga ( ) = ( ) + .

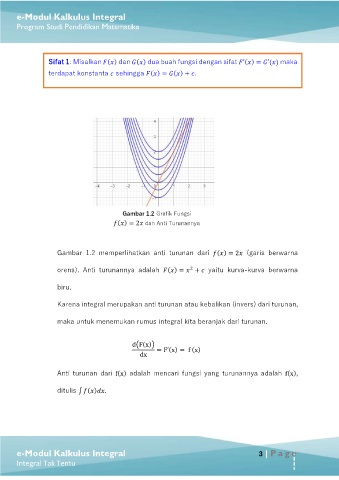
Gambar 1.2 Grafik Fungsi

( ) = 2 dan Anti Turunannya

Gambar 1.2 memperlihatkan anti turunan dari ( ) = 2 (garis berwarna

2
orens). Anti turunannya adalah ( ) = + yaitu kurva-kurva berwarna

biru.

Karena integral merupakan anti turunan atau kebalikan (invers) dari turunan,

maka untuk menemukan rumus integral kita beranjak dari turunan.

d(F(x))
= F’(x) = f (x)
dx

Anti turunan dari f(x) adalah mencari fungsi yang turunannya adalah f(x),

ditulis ∫ ( ) .

e-Modul Kalkulus Integral 3 | P a g e

Integral Tak Tentu