Page 77 - Buku Teks Digital Mate KSSM T5

BAB 2 Matriks

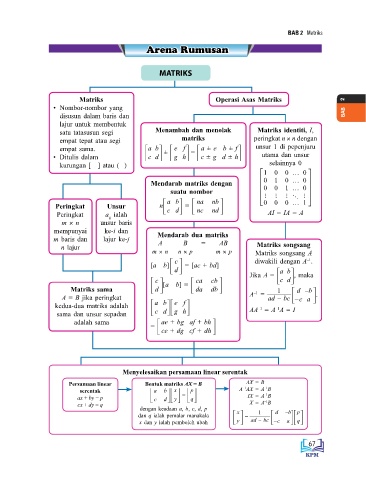
Arena Rumusan

MATRIKS

Matriks Operasi Asas Matriks 2
• Nombor-nombor yang
disusun dalam baris dan BAB
lajur untuk membentuk
satu tatasusun segi Menambah dan menolak Matriks identiti, I,
empat tepat atau segi matriks peringkat n × n dengan
a b
e f
empat sama. 3 4 3 4 3 a ± e b ± f 4 unsur 1 di pepenjuru
=
±
• Ditulis dalam c d g h c ± g d ± h utama dan unsur
kurungan [ ] atau ( ) selainnya 0
1 0 0 … 0
Mendarab matriks dengan 0 1 0 … 0
suatu nombor 0 0 1 … 0




a b
=
Peringkat Unsur n 3 4 3 na nb 4 0 0 0 … 1
c d
nd
nc
Peringkat a ialah AI = IA = A
ij
m × n unsur baris
mempunyai ke-i dan Mendarab dua matriks
m baris dan lajur ke-j A B = AB
n lajur Matriks songsang
m × n n × p m × p Matriks songsang A
c
–1
[a b] 3 4 = [ac + bd] diwakili dengan A .
d
a b
3 4
c
3 4 [a b] = 3 ca cb 4 Jika A = c d , maka
Matriks sama d da db 1 d –b

–1
A = B jika peringkat A = ad – bc3 – c a 4 .
e f
a b
kedua-dua matriks adalah 3 43 4 AA = A A = I
–1
–1
sama dan unsur sepadan c d g h
adalah sama = 3 ae + bg af + bh 4
ce + dg cf + dh
Menyelesaikan persamaan linear serentak
Persamaan linear Bentuk matriks AX = B AX = B
–1
–1
serentak a b x = p A AX = A B
–1
ax + by = p 3 c d 43 y4 3 q4 IX = A B
–1
cx + dy = q X = A B
dengan keadaan a, b, c, d, p
x
p
–b
d
1
dan q ialah pemalar manakala 3 y4 = ad – bc 3 – c 43 q4

x dan y ialah pemboleh ubah a
67
KPM